夏至 | 秘密分享，也可以是量子的

在许多谍战电影或悬疑剧情中，我们常常看到这样的桥段：一份高度机密的文件被撕成几份，分别交由不同的人保管。有的藏在保险柜里，有的缝进衣物夹层，还有的通过口令或暗号秘密传递。单独掌握其中任意一份都无法解读全部内容，唯有多方联合，才能拼出完整的信息。

这一叙事背后，隐含着一个密码学中的基础思想，即秘密分享^[1,2]。这是一种将机密信息拆分成多个无用片段，再分别托管于不同参与者之间的分布式策略。任何个体无法单独恢复原始内容，只有当足够数量的参与方协作时，才能还原出完整的秘密。

在经典密码学中，这一机制已经发展成熟，广泛应用于分布式密钥管理、安全计算和去中心化网络设计。然而，将其推广至量子信息领域却并不简单。量子态无法被复制，测量会引起不可逆的坍缩，传统手段面临根本障碍。但另一方面，量子力学也提供了全新的解决路径。

这便是我们今天将要深入探讨的话题——量子秘密分享（Quantum Secret Sharing, QSS）。通过量子纠缠所构建的全局关联结构，即使每个参与者单独无法获取信息，多方的协同操作仍然可以高效安全地恢复出所需数据。

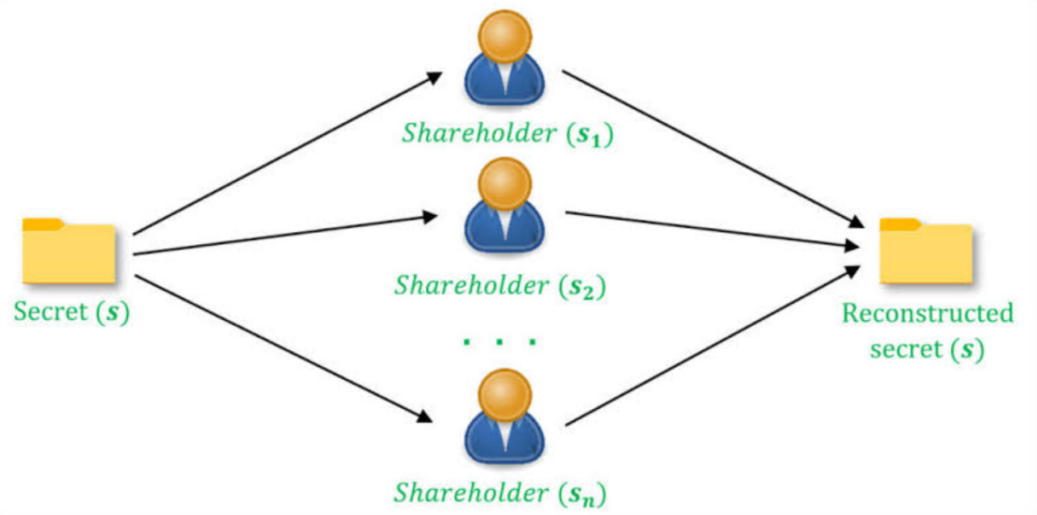
图1. 秘密共享方案的基本原理

图源：网络

早在1999年，Hillery、Bužek 和 Berthiaume 就提出了一个惊人的想法^[3]。他们建议利用三粒子纠缠态实现秘密分享，这个态被称作 GHZ 态，它看起来是这样的：  。我们可以这样想象，Alice、Bob 和 Charlie 分别持有这个纠缠态中的一个粒子。由于三者处于纠缠态，它们的状态无法独立描述，整体行为超越了任何单独粒子的视角。

当 Alice 想分享一个比特，比如“1”，她可以在自己的粒子上施加一个相位操作，将 GHZ 态变为  。随后三人分别在约定的基底上测量各自的粒子，每个人的测量结果看似完全随机，但只要 Bob 和 Charlie 合并他们的信息，就能判断出 Alice 究竟编码了“0”还是“1”。这个过程的关键在于，信息不是藏在任何一个粒子中，而是分布在整个系统的纠缠结构之中。单独持有粒子的任何一方都无法获取关于秘密的任何信息。

量子秘密分享的真正威力，在于它不仅能分享经典信息，还能分发完整的未知量子态^[4]。在经典通信中，信息可以随意复制。但在量子世界中，由于不可克隆定理，量子态无法被完美复制。为此，科学家设计了一类特殊的编码方式，将一个量子比特的状态分散到多个粒子上，只有满足一定门限的参与者才能恢复出原始态。

比如著名的五量子比特码，可以将一个任意量子态编码为五个粒子的联合态。任何少于三人的子集都无法恢复出初始态，只有达到门限的参与者，才能通过测量和纠错，重新得到完整的量子信息^[5,6]。这种机制为未来的分布式量子存储和安全通信提供了可靠的工具。

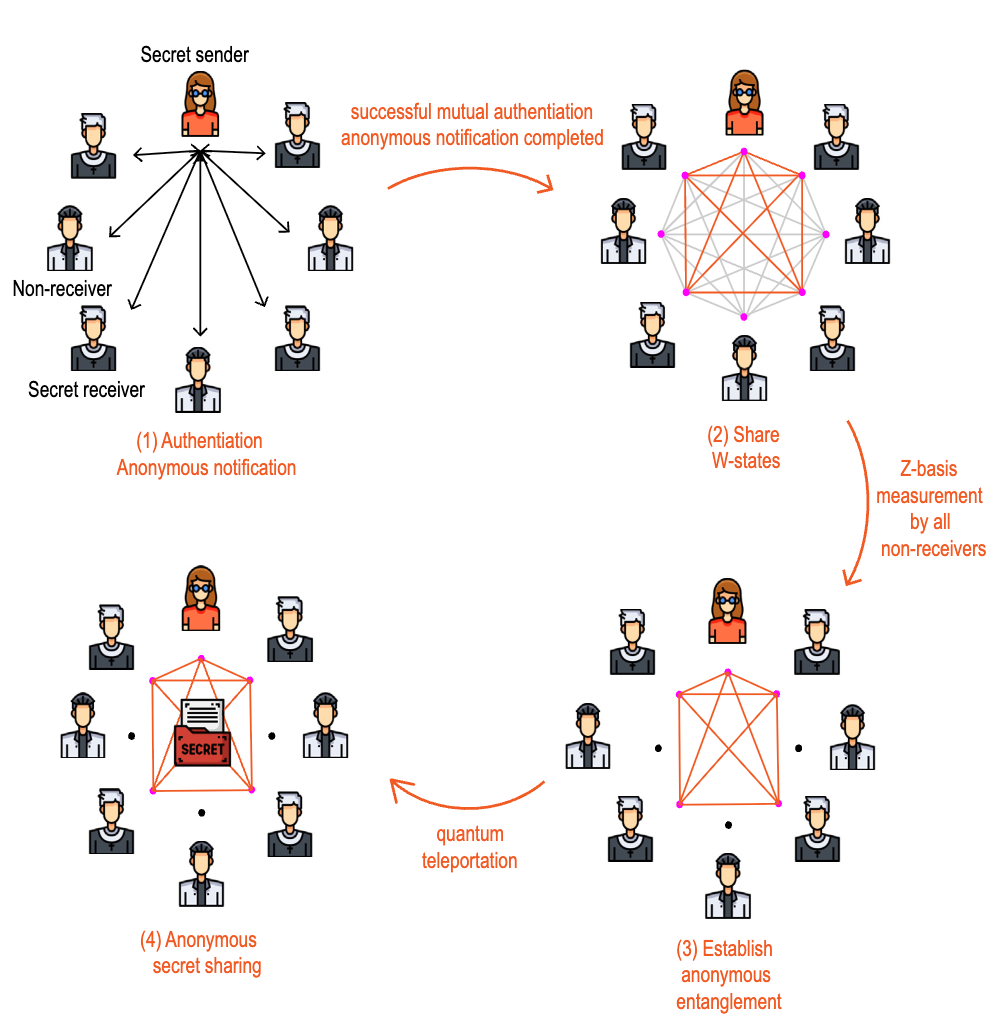
图2:. 利用量子态实现匿名安全通信的增强型量子秘密共享协议示意

图源：网络

如果我们能在秘密分享的同时直接对秘密执行计算，那么将极大拓展其应用边界。在经典领域，这类技术被称为同态秘密分享^[7]：参与者各自在本地处理自己的份额，最后的计算结果仍是正确函数值的拆分，且过程中的信息始终未被泄露。

在量子领域，这一思想也正在被逐步实现。通过量子编码后的结构，研究人员设计出一类能在秘密状态上直接施加量子门操作的方法。尽管目前仅限于部分基础门的实现，如异或和简单的控制门，但已经为构建量子安全多方计算和量子云计算奠定了理论基础。

量子秘密分享的核心优势，在于它的安全性来源于物理原理本身，而非算法的复杂性。这意味着，即便攻击者拥有无限计算能力，只要手中份额不足，仍无法获取任何有用信息。这一特性使其成为高安全性分布式系统的理想选择。无论是用于量子密钥托管、抗泄漏的分布式存储，还是在量子云计算、量子电子投票、多方量子签名等场景中，门限量子秘密分享都能为系统提供稳固的信任基础^[8,9]。

放眼未来，量子秘密分享有望成为量子网络的底层协议之一，就如同 TCP/IP 构建了互联网的基础一般，为量子互联网的安全性与可扩展性提供强有力的支撑。

[1] Shamir A. How to share a secret[J]. Communications of the ACM, 1979, 22(11): 612-613.

[2] Blakley G R. Safeguarding cryptographic keys[C]//Managing requirements knowledge, international workshop on. IEEE Computer Society, 1979: 313-313.

[3] Hillery M, Bužek V, Berthiaume A. Quantum secret sharing[J]. Physical Review A, 1999, 59(3): 1829.

[4] Cleve R, Gottesman D, Lo H K. How to share a quantum secret[J]. Physical review letters, 1999, 83(3): 648.

[5] Bell B A, Markham D, Herrera-Martí D A, et al. Experimental demonstration of graph-state quantum secret sharing[J]. Nature communications, 2014, 5(1): 1-12.

[6] Mouzali A, Merazka F, Markham D. Quantum secret sharing with error correction[J]. Communications in Theoretical Physics, 2012, 58(5): 661.

[7] Boyle E, Gilboa N, Ishai Y, et al. Foundations of homomorphic secret sharing[J]. Cryptology ePrint Archive, 2017.

[8] Schoenmakers B. A simple publicly verifiable secret sharing scheme and its application to electronic voting[C]. Advances in Cryptology—CRYPTO'99, Santa Barbara, California, USA,1999:148-164.

[9] Desmedt Y, Frankel Y. Shared generation of authenticators and signatures[C]. Advances in Cryptology-CRYPTO'91, Santa Barbara, Califoria, USA, 1992:457-469.

图 | 陈春萌

文 | 张婷