PNAS研究揭示合作的时序特征：枢纽节点越晚参与越有利于合作演化

摘要

在复杂多变的社交网络中，如何让合作的种子生根发芽？传统的观点告诉我们，应该抓住网络中那些人脉广、影响力大的社交枢纽。只要驱动他们率先展开合作，便能引领合作潮流。然而，来自PNAS的一项最新研究却提出了一个颠覆性的观点：想要促进集体合作，最佳策略或许是让这些“大人物”们最后出场。

这项研究将目光从静态的网络结构转向了动态的交互顺序，通过严谨的数学推导和多组实证数据分析发现，当互动由社交圈子较小、关系更紧密的群体先行发起，奠定合作基础后，再让枢纽节点加入，合作的门槛将显著降低。

如果你对这一话题感兴趣，给你推荐我们最近刚刚发布的「AIX传播」主题读书会，读书会发起人之一深圳大学长聘副教授廖好老师策划了智能传播模块，会专门围绕“信息与计算视角的智能传播”和“社交网络中传播影响力最大化问题研究”两个主题进行研讨，欢迎你的加入。

关键词：静态网络，时序网络，演化博弈论，枢纽节点，爆发式交互

王薏潮丨作者

周莉丨审校

论文题目：Promoting collective cooperation through temporal interactions 

论文地址：https://www.pnas.org/doi/10.1073/pnas.2509575122

1. 背景介绍

理解集体合作的演化机理至关重要，现有的绝大多数合作演化研究都是基于静态网络的假设，这意味着网络链接一旦建立便永久存在，对互动发生的先后顺序毫无考虑。但现实生活中的接触往往是短暂且间歇的：邮件往来、展会交流、医院就诊乃至办公室内茶水间的交谈，都在不断生成和消失的时序网络中进行。并且，通常情况下人们普遍认为，在人际互动中，“越中心越重要”，社交圈层越广的人，应当率先展开合作。

然而，这项最新发表于PNAS的研究分析了合作在任意时序网络中的传播机制，发现要想激发群体合作，反其道而行之更有效：应当让社交枢纽（拥有大量链接的人）排在后面参与。这样一来，先由“社交小圈”打头阵，奠定合作基础，再让“关键节点”加入，就能显著降低合作门槛，推动利他行为在群体中更高效地扩散。根据此发现，研究者提出了在时序网络中重排交互顺序以促进合作的方法。

研究者首先从理论上推导出了合作在任意时序网络上涌现的数学条件，并进一步通过多组实证数据集，验证了重排交互顺序是促进合作的有效方法。

2. 合作的演化博弈模型介绍

考虑了一个演化博弈模型，如下图所示，个体间的博弈连边关系会随时间变化（图 1A）。将所有时刻的交互快照合并，可以得到一个聚合的静态网络（图 1B），称为“替代网络”（replacement network）。

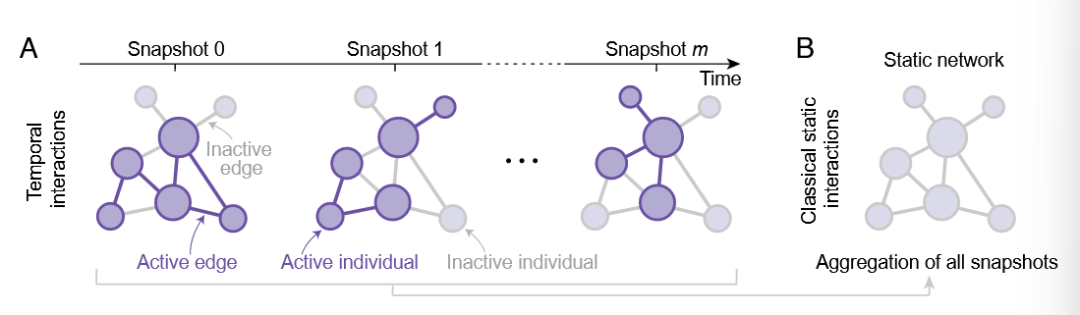
图1A. 个体间博弈随时间变化的快照，图1B. 聚合而成的静态网络

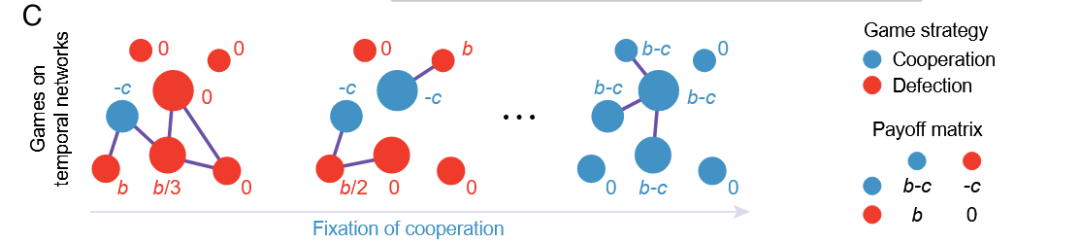
图1C. 博弈框架模型，每位个体与所有交互伙伴逐一博弈，以计算自身的平均收益

图1C 展示了博弈模型框架，在该模型中，每个个体在任意时刻都可选择两种策略之一：合作或背叛。研究者采用了经典的捐赠博弈框架，在这一框架下，每位个体都会与其所有交互伙伴逐一进行博弈，并据此计算自身的平均收益。选择合作的个体需要为对方支付一定代价，以便让对方获得相应的好处；选择背叛的个体则无需付出任何代价，也不会为对手带来任何利益。这种对成本与收益关系的刻画方式，是成对博弈中描述社会困境时广泛使用的规范化表达。这里收益的设置形式是一种平均收益，个体参与了多少个博弈，获得的总收益要除以参与博弈的个数。简言之，个体的收益不是参与的博弈的收益累计，而是从参与的博弈中获得的一种归一化收益，这也意味着不是参与的博弈数量越多越好。图 1C的第三个快照很好地说明了这一点，拥有三条边中心节点获得的收益与其相连的仅拥有一条边叶子节点相同。

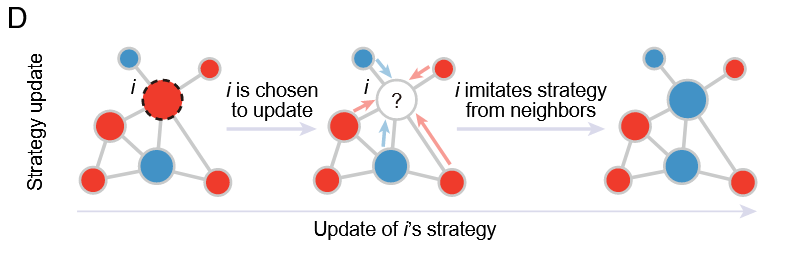
图1D. 基于模仿的更新机制描述策略演化过程

如图1D所示，研究者采用了一种基于模仿的更新机制来描述策略演化过程：每次更新时，首先从全体个体中随机选出一人，然后让其从所有邻居中挑选一位作为模仿对象，并将该邻居的策略复制过来。邻居被选中的概率与其“适应度”成正比，适应度由邻居在过去博弈中获得的平均回报按一定强度放大后，加上一个基础值共同决定。这样，收益更高的邻居更容易被模仿，而随机成分又保证了策略更新的多样性和不确定性。

本文有对策略更新过程进行详细的补充说明，文章中称之为演化过程（ Evolutionary Process）。 实际上，这里采用的是一种利于解析求解的 “死亡—出生／模仿”（death–birth or imitation）更新框架。具体步骤如下：

1. 每个时间步（snapshot 持续 N 次更新，这里 N 是个体总数，以保证平均每人更新一次），先完成一次全体两两博弈并计算每个个体的平均收益。

2. 从群体中均匀随机选出一个个体“死亡”——即放弃当前策略。

3. 该位置由其所有“邻居”（在替代网络上与其相连的那些个体）中某个邻居以特定概率来“繁殖”，这就是一个策略模仿更新过程。

这里可能是为了便于对阈值的精确推导，从而模仿更新规则没有采用模拟中更常见的Fermi规则。不过值得一提的是，本文的补充材料中也验证了对比复制（包括 Fermi 规则）与模仿更新下，如果按相同“枢纽优先级”重排快照序列，合作阈值也同样可以得到优化，这里感兴趣的读者可以自行查看（SI Appendix, section S4）。

此外，还要补充的是，这里是一种异步更新（Asynchronous Imitation），并且引入了突变机制：在一个本质上是全合作者或全背叛者的群体里，随机挑一个位置 i 改成相反的策略。这个突变位置 i 被选中的概率是均匀的 1/N，且每次只有一个突变体出现。突变机制的引入，是因为整个系统会容易达到全合作者和全背叛者的吸收态，由于系统中策略完全来源于模仿，吸收态是一个很明确的演化终止条件。

于是，结合我们之前的时序网络快照，整个演化博弈系统的设定可以这样理解：在这一模型中，整个演化过程可看作从一次突变开始，即群体原本全为同一种策略，随机选中一人改变其合作或背叛行为。随后，网络按照一系列离散的时间快照依次切换：在每个快照阶段，个体一个快照内进行N次博弈演化（每次演化包含一次全局收益计算和一次单点策略更新），每人平均更新一次后便进入下一快照。如果在任意时刻所有个体都趋于同一策略，即形成吸收态，本轮演化结束，并记录合作突变或背叛突变最终占据全体的概率，文中称为固定概率。接着再次以同样方式引入新突变，重复上述循环。在弱选择条件下，当合作突变的固定概率高于背叛突变的固定概率时，即表明合作策略在这个动态时序网络中具有进化优势。

3. 时序网络上合作演化的条件

研究者这里用随机游走和溯祖过程（coalescent process，也可译为谱系汇合）的方法，为时序网络中的合作演化给出了一个普适性的条件。合作策略能否胜出，取决于一个核心的权衡：合作者为自身带来的直接收益，是否大于其策略在“二阶邻居”层面竞争时所带来的间接收益，如下式所示

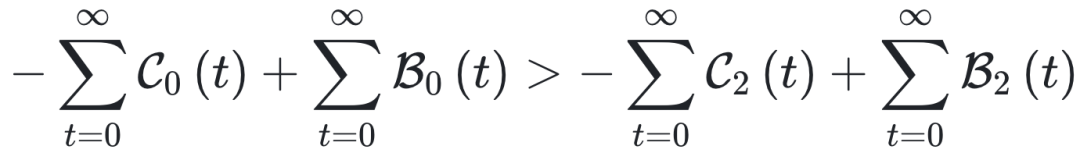
这里， 代表了合作者在“零步随机游走”阶段（也就是只考虑自身或直接邻居交互）所承担的累计预期成本，表示合作者通过捐赠博弈在直接接触（零步）中获得的直接收益。公式右侧符号含义同理，整体含义是一个合作者，在两步随机漫步的距离外，给其“二阶邻居”  带来的总预期净收益，这可以反应合作策略通过“帮助邻居的邻居”而获得的间接传播优势。 t 从 0 累加到无穷表示从突变出现到最终稳定或灭绝这整个演化周期里合作者的总成本。在数学上，由于谱系汇合概率随 t 增大而衰减，这个无穷和是收敛的。

如果在长期累积下来，合作由直接交互为自身带来的净收益要比给二阶邻居的净收益要好，那么在这个时序网络上，合作策略就会被自然选择偏好。

4. 量化枢纽节点参与互动的优先级

上述理论结果能告诉我们合作在什么条件下得以胜出，但针对”如何在真实网络中去设计交互顺序”这一实际问题，则需要进行更深入的研究。首先，需要我们弄清楚的问题是：在社会互动中，究竟是早期互动占据的影响力更大？还是更晚发生的互动影响力更大呢？研究者通过对一个实证数据集以及系谱汇合概率来解答这一问题。

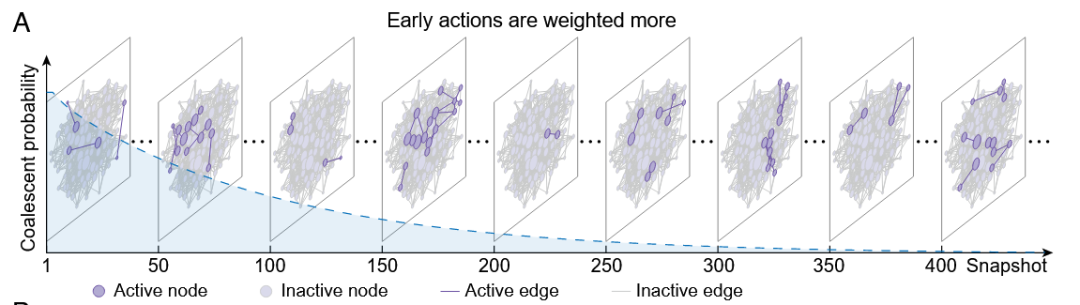
图2A. 办公楼中面对面接触数据集时序快照的系谱汇合概率变化趋势

图2A 这一子图展示了基于办公楼中面对面接触数据构建的时序快照序列，步数 0–49：对应“快照 0”（Snapshot 0）内的 50 次异步更新，此时网络结构固定不变。步数 50–99：对应“快照 1”内的 50 次异步更新，网络结构切换到 Snapshot 1 后再保持不变。以此类推，每隔 N 步就进入下一个快照阶段。每个快照中活跃的节点和边以紫色标出。这里，令 T^coal 为两条谱系第一次汇合所需的随机步数，则 Pr[T^coal≤t] 就是它们在最多 t 步内合并的概率，也就是虚线所表示的系谱汇合概率。这张图实际上给出了“第 t 次更新”对整个演化结果的重要性权重。图中这个系谱汇合概率呈现出衰减趋势，在决定演化结果时，时间上更早发生的互动比更晚发生的互动具有更大的影响力。

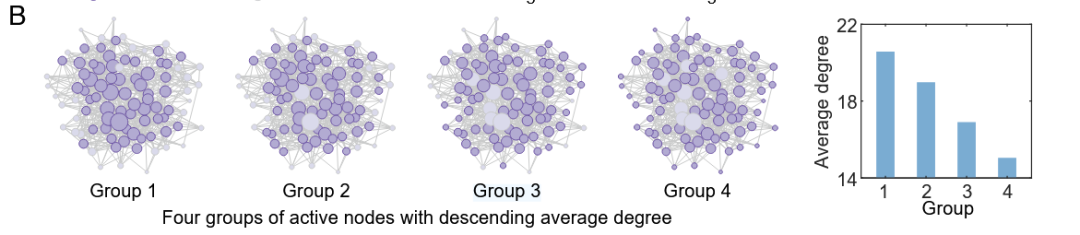
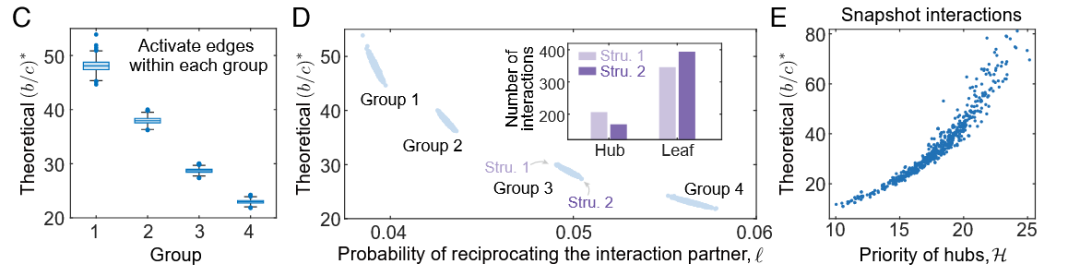
图2B、C、D. 将替代网络等分为四组，分析节点度和互惠概率对合作演化的影响

在定义枢纽优先级 H 来量化每个时间快照中“关键节点”参与互动的优先顺序之前，我们需要准确判断这个优先级指标 H 应该与哪些因素相关。首先可以想到的是节点度，一般而言，节点度越大代表该节点越是枢纽（Hub），影响力也就越大。 为方便后续分析节点度对合作演化的影响，研究者在最终聚合的“替代网络”上，将所有节点按度数从高到低排序，并等分为四组（Group 1–4）。图2B 中柱状图展示了这一设置，Group 1–4 的平均节点度依次递减。图2C中，对上述的每一组的子网络，以概率 P=0.5 随机激活底层聚合网络中的边，再计算合作被偏好所需的临界收益—成本比 (b/c)^*(这个值相当于是一个“合作临界门槛”)。结果表明，平均度越高的组 (Group 1) 具有更高的临界收益—成本比，即更难以推动合作，而平均度越低的组的合作门槛越低。另一个影响因素则是节点在快照中“互惠”其合作伙伴的概率，如图2D所示，曲线显示随着增大，合作门槛明显下降。以 Group 3 为例，进一步将节点分为度数前 20% 的Hub节点和其他叶子节点，对比在“Hub节点参与多”与“Hub节点参与少”两种结构下的交互次数与临界收益—成本比，结果表明，Hub节点参与越少，合作门槛越低。

因此，基于快照中活跃节点的平均度 q 和互惠概率，这里定义了枢纽优先级指标

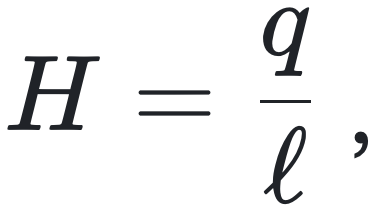
这里这个枢纽优先级指标 H 是一个很重要的量，其直接衡量枢纽节点（即度值高的 Hub节点）的参与程度，越大参与程度越强。后文这个指标还会反复出现。将每个快照的 H 与对应的临界收益—成本比作散点图，结果呈正相关：H 越低（即枢纽参与越少、叶节点先行），临界收益—成本比越低，合作越易涌现（图2E）。

进一步可以推导得出“任何时序交互下”合作获胜所需的临界收益-成本比可以作如下近似表示：

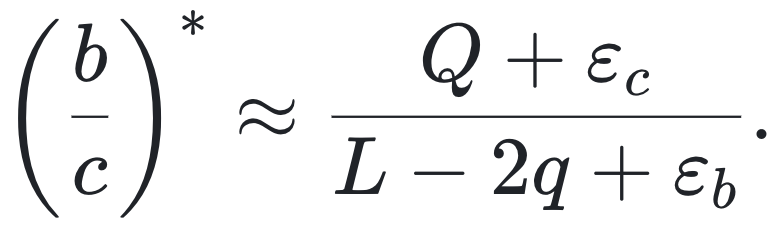
这在理论上保证了，若让具有较少社会连接的节点（即低 q）和高度互惠的交互（即高）尽早发生，就能显著促进合作的涌现这一结论。这里以基于优先连接机制生成的 Barabási–Albert 时序网络为例：按自然加入顺序，枢纽节点（大度数）先行互动，合作门槛最高；若将序列完全颠倒，即让小度数节点先互动，则合作所需阈值大幅下降。

5. 基于量化指标优化时序交互 

a. 实证网络和人工网络

前文给出的指标和结论是否在真实的时序交互中成立? 作者这里首先利用了四组实证网络数据（图3A）说明：真实交互序列中枢纽参与先后无规律，可通过简单排序实现“弱化”枢纽参与早期交互，这将为合作演化创造更有利的时序条件。

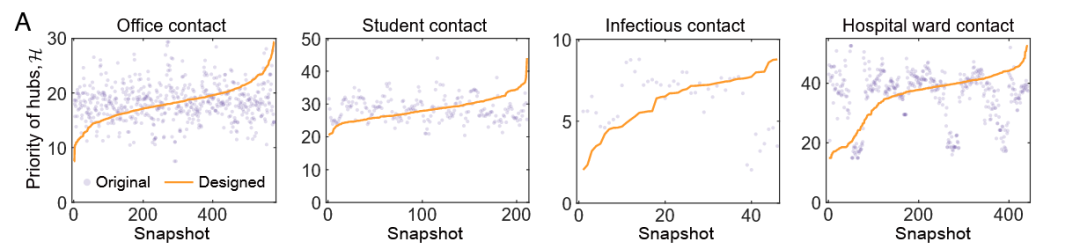
图3A 四组分别代表办公室、高中、展会和医院的实证网络数据，紫色点表示原始四组实证网络（办公室、高中、展会、医院）中，每个快照的 H 值呈现高度波动与随机分布；橙色曲线表示将快照按 H 从小到大排序后得到的“设计”序列。

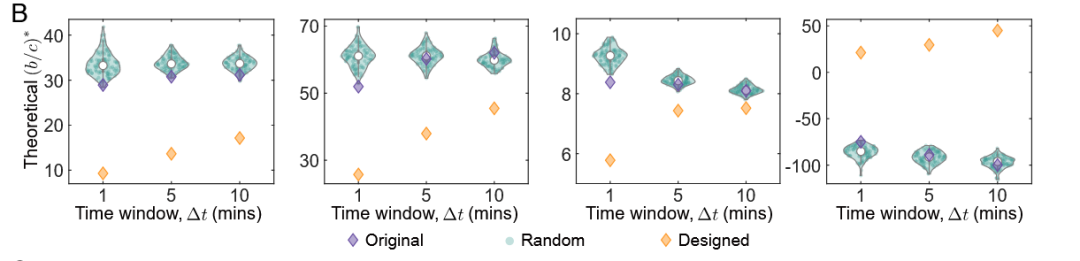
图3B. 不同序列下临界收益—成本比的分布情况的可视化

图 3B 中的小提琴图用于比较三种交互序列在不同时间窗口下合作所需的临界收益—成本比的分布差异。图中：

• 青绿色的轮廓描绘了随机序列在多次打乱后所得到的核密度估计，轮廓越宽表明该临界收益—成本比值在随机置换中出现的频率越高；

• 白色小圆点标示了这一分布的中位数 (或者均值)，便于把握其集中趋势；

• 紫色菱形对应原始交互序列的临界比值，通常位于随机分布的内部；

• 橙色菱形则代表按“枢纽优先级”升序重排后的交互序列，其临界比值在所有时间窗口上都显著低于原始和随机序列。

横轴为聚合交互所用的时间窗口长度（以分钟为单位，例如每隔一分钟聚合一次交互）。该图清晰表明，通过先让度数较低的节点参与、再让枢纽节点加入的排序方式，可以普遍降低合作门槛，甚至在原本不利于合作的情境中，也能逆转局面，实现合作策略的演化优势。

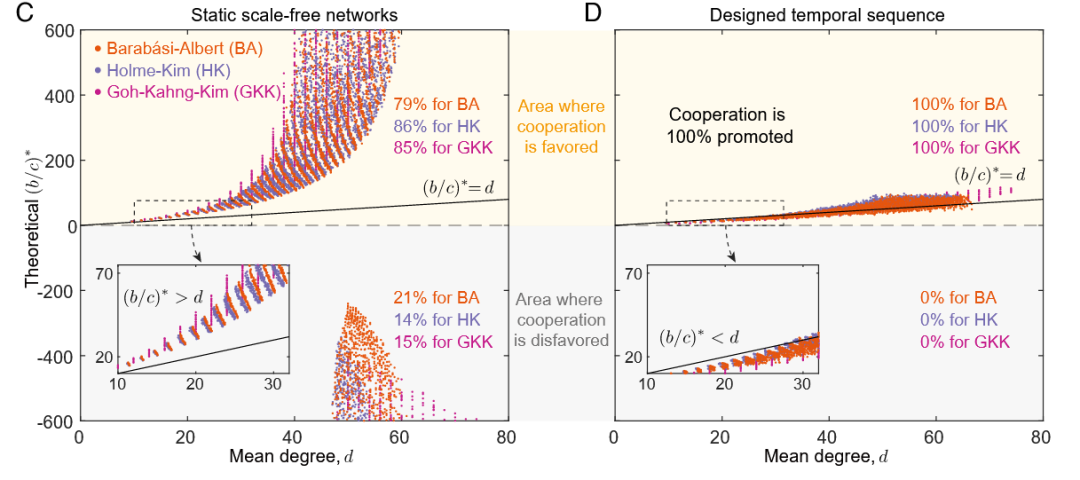
图3C、D.基于H值优化三种典型网络BA、HK、GKK的时序交互特征

进一步地，研究者在这里考虑了三种典型的人工网络，证明即使连真实的时间顺序都不可得，只要把静态网络的每条边当做“快照”来看，并按枢纽优先级从低到高排列，就能从根本上改写无标度网络对合作的不利局面。这里，节点的平均度为横坐标、临界收益-成本比为纵坐标，散点表示每一次网络实例的计算结果，并以“临界收益—成本比等于平均度”这条基准线来对照：当散点落在线上方时，说明合作所需条件比同质网络更苛刻；落线下方则表示合作门槛低于基准，有利于利他行为涌现。

这里，每一个散点都代表在给定平均度下，一次独立网络实例计算出的临界收益—成本比，即 (b/c)^* 值。

• 当点高于黑线时，(b/c)^*>d，说明在该静态网络中合作阈值高于基准，合作被抑制；

• 当点低于黑线时，(b/c)^*<d，说明该实例有利于合作。

对比结果表明，在自然时序下的无标度网络，大多数实例的散点位于基准线以上，合作几乎难以实现；而在经过“先弱后强”顺序优化后，所有实例的散点都紧密分布在线下或正好在线上，且经过时序重排后，无一例外，所有网络实例的合作门槛都不高于均质网络的基准值（即平均度），且多数情况下甚至低于这一基准。

b. 爆发式交互网络

在现实社会网络中，人们的交互往往不是均匀分布，而是一段时间内可能频繁接触，随后又长时间无任何互动，这种“爆发—静默”交替出现的行为模式称为爆发式（bursty）交互。研究者同样考察了在这一接触模式下，时序交互对合作演化的影响。

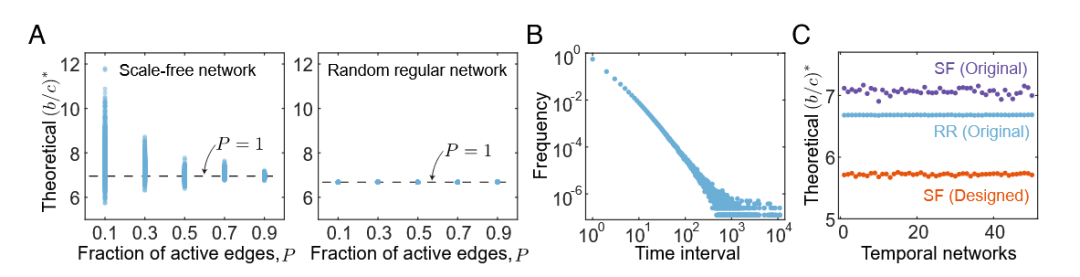
图4A、B、C. 无标度网络和随机规则网络中边的激活比例对合作阈值的影响

研究者首先在两类典型网络中检验了随机激活交互边比例对合作门槛的影响。通过在每个时间步以比例 P 随机激活网络中的边，生成一系列瞬时交互网络，并计算合作被偏好所需的临界收益—成本比 (b/c)^*发现，在无标度网络上，不同的交互结构（即不同的 P）会显著改变临界收益—成本比，尤其是在 P 较小时；而在随机规则网络上，临界收益—成本比几乎不随 P 变化”。 在高度异质的无标度网络里，不同的激活比例会显著改变合作所需的最低回报成本比，尤其在活跃边很少时，合作阈值大幅抬高；而在同质的规则网络中，该阈值几乎不受激活比例变化的干扰.

接着，本文进一步分析了“爆发—静默”式互动的时间间隔，发现两次接触之间的停顿期分布呈重尾特征，即短期内频繁爆发的交流与偶尔出现的长时间沉默交替出现，完全符合幂律分布的规律。图4B对爆发式交互事件的“间隔时间”分布时序特征做了直观展示。

最后，通过将网络快照按照枢纽节点参与重要性升序重排，研究者重新计算了无标度网络的合作阈值，结果显示原本集中在 7 左右的门槛被稳定压低至 5.5 左右，充分说明仅凭调整交互先后顺序就能在不改变网络结构的前提下，大幅增强利他行为的涌现。这里通过图4C展示，图中横轴表示不同的爆发式交互实例编号（共 50 次）。紫色点（SF Original）表示无标度网络原始时序下，不同随机爆发序列的临界收益—成本比散点。蓝色点（RR Original）表示随机规则网络原始序列下的临界收益—成本比。橙色点（SF Designed）是对无标度网络按 H 升序排序后的临界收益—成本比。

c. 时序高阶网络

在时序超网络（temporal hypernetworks）中，即每个快照中的群组交互由超边来刻画，H值依然有效吗？这里为体现高阶网络对多人博弈互动的刻画，博弈结构使用了能体现多人群组互动特点的公共物品博弈，整个博弈交互演化与之前的两两交互的博弈过程是类似的，图4D说明了这一过程。随后，研究者基于此实验设置重新做了理论推导和模拟，并将结果展示为如下四张图E、F、G、H。

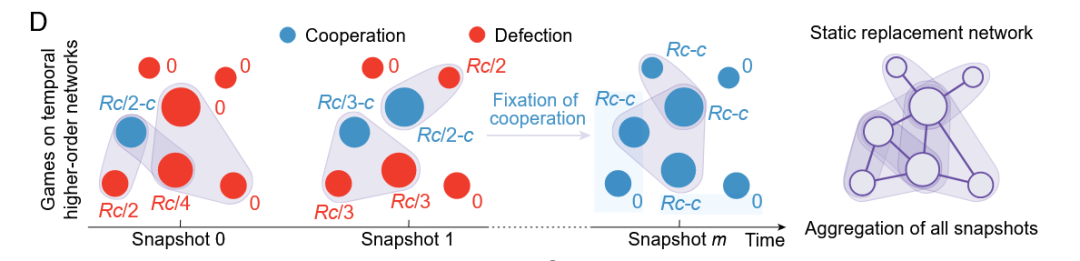
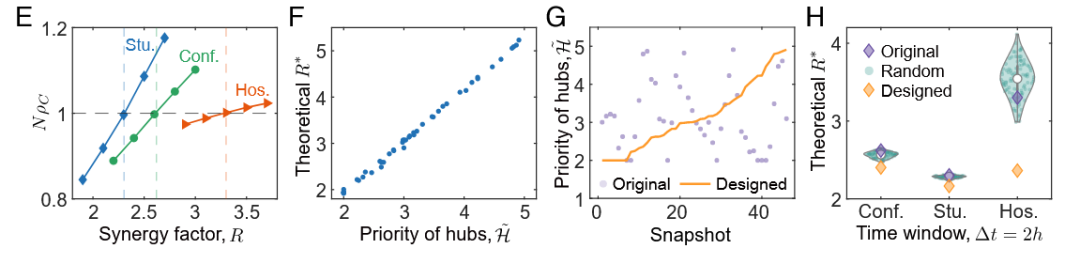
图4D、E、F、G、H. 基于量化指标优化高中、会议和医院三种时序超网络的结果分析

在这里，研究者利用了高中、会议和医院三组实证高阶交互数据来进行分析，同时还定义了与两两交互的网络相类似的超网络枢纽优先级指标，在后续以这个指标为依据进行重排。图 4E 展示了理论预测的准确性。其中，横轴对应公共物品博弈中的增益因子，纵轴表示合作策略最终固定于群体的概率。彩色虚线是计算出的临界增益因子 (这是公共物品博弈中的重要参数，其作用类似于两两交互时的收益-成本比 b/c，用于衡量社会困境的强弱)，只有当增益因子超过这一阈值时，合作才会被偏好；实线则展示了数值模拟得到的合作固定概率（即前文的合作突变或背叛突变最终占据全体的概率，由于单个体突变的概率为 1/N，所以这里乘上群体规模 N 以反映群体的合作固定概率），可以看到在固定概率为 1 时的散点值恰好在理论计算的虚线上。随后，通过揭示了枢纽参与优先级与临界增益因子之间的线性正相关关系（图4F）。

类似地，研究者展示了如何通过对快照按枢纽优先级升序重排来重构交互顺序（图4G）。最后，图 4H则证明了这种重排策略能够在所有数据集中普遍降低合作的临界增益因子阈值，进一步验证了所提出的时序设计方法在多种真实高阶交互情境下的有效性。

上述结果表明，对于时序高阶网络，不仅能做类似的理论分析和实验设计，并且得出的结论仍然适用的，按超网络中定义的枢纽优先级的“升序重排快照”，即先执行优先级最低（枢纽最少）的快照，再逐步到优先级最高的那部分，能有效降低合作门槛。

6. 总结

与将个体策略与网络结构共同演化的共演化模型不同，本研究仅关注网络链接随时间变化所形成的时序快照，这些快照直接来源于真实接触数据，并与策略演化过程相互独立。研究者通过谱系汇合分析严格推导出了合作相对于背叛获得进化优势所需的最小回报与付出比，并将这一条件推广到群组公共物品博弈中。为量化各个时间快照中关键节点介入的重要性，他们提出了枢纽优先级指标，用以衡量何时让枢纽节点参与最不利于合作。基于此发现，将快照按枢纽优先级由低到高排序，即先让度数较低但社交关联广泛的节点参与，再让最具影响力的枢纽节点最后加入，能够显著降低合作门槛，使利他行为在群体中更高效地扩散。这一原则在人工生成的无标度网络与随机规则网络，以及办公室、高中、会议和医院等多组实证接触网络中均得到验证，并且在爆发式交互和高阶群组互动等扩展情境下依然有效，数值模拟结果与理论预测高度吻合。

这项研究不仅为我们理解复杂系统中的合作提供了新的理论视角，也为现实世界中促进协作提供了切实可行的策略。从企业管理中的团队组建，到公共卫生事件中的信息传播策略，再到线上社区的氛围营造，通过精心设计网络中个体互动的时序特征，我们或许能用更低的成本，激发更大范围的善意与合作。

在AI快速发展的当下，AI不仅深刻影响着信息传播的方式，也为传播学研究带来了全新视角和方法。基于此，集智俱乐部联合北京师范大学许小可教授、浙江大学张子柯教授、南京大学王成军教授、深圳大学廖好副教授共同发起“AI×传播”读书会，从计算叙事、智能传播、人机传播与传播仿真四个板块向来共同探索AI与传播的前沿交叉，来深度理解传播机制和传播生态。读书会自8月23日起，每周六10:00-12:00举行，预计持续12周。欢迎扫码加入，共建“AI×传播”社区。

6. 高考分数只是张入场券，你的科研冒险在这里启航！

7. 系统科学前沿十讲：理解自然、生命与社会的复杂性