DRUGAI
今天为大家介绍中国石油大学计算机科学与技术学院宋弢教授团队发表在Advanced Science的文章《Programmable DNA-Based Molecular Neural Network Biocomputing Circuits for Solving Partial Differential Equations》,这篇论文的主要内容是提出一种基于增广矩阵的DNA分子神经网络框架,首次实现了生物偏微分方程(PDE)的分子级求解,该框架通过三个关键创新突破现有技术局限:(1)设计基于DNA链置换反应的增广矩阵编码策略,将神经网络权重映射为DNA链浓度比例,利用链置换级联反应实现多维参数组合输出;(2)将膜扩散理论与除法运算理论融入DNA电路架构,开发出支持空间微分过程的偏导数分子计算模块;(3)构建基于误差反馈机制的DNA分子自适应神经网络系统,实现权重参数的迭代优化。本研究提出了一种新型智能非硅基计算架构,为未来生物计算机及生命科学领域的非传统计算装置提供了理论依据和潜在应用范式。

介绍
偏微分方程(Partial Differential Equations, PDEs)是刻画物理、生物与工程系统动态行为的核心数学工具,其高效求解对气候建模、药物扩散模拟等关键领域至关重。然而,传统数值方法(如有限元法FEM、有限差分法FDM)在求解高维非线性PDE时遭遇根本性挑战:计算复杂度和计算成本随维度增加呈现指数级增长(维数灾难)。近年来,生物分子系统因其天然的并行性与高能效特性备受关注,为基于生物分子系统的非传统计算范式提供了新路径。DNA分子通过链置换反应实现的可编程计算能力和并行计算能力,为连续空间微分运算提供了新思路——通过分子浓度的梯度分布与动态反应网络,有望直接映射PDE的微分算子,规避传统离散化带来的精度损失。这种生物-物理融合的计算架构,为发展新一代PDE求解器提供了突破传统计算复杂度边界的可能性。
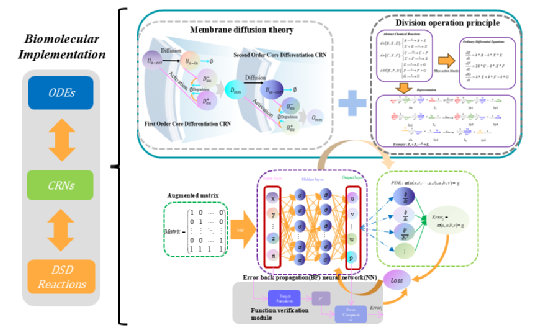
图1:基于DNA的分子神经网络生物计算电路实现偏微分方程求解
基于CRNs的多组合参数并行输出神经网络
图2描述了基于增广矩阵的误差反向传播神经网络结构。基于左侧子图描绘的增广矩阵,基于乘法运算,能够间接控制神经网络的输入参数设置,进而实现神经网络关于多组合参数项的输出控制。右侧子图为基于误差反向传播的全连接神经网络。
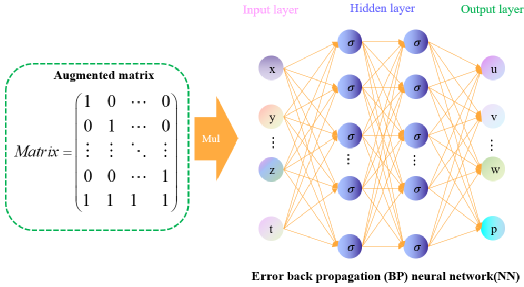
图2: 基于CRNs的多组合参数并行输出神经网络
基于CRNs的偏导数计算原理
针对单变量项偏导数计算,图3所示的基于膜扩散思想的偏微分求导CRN过程主要包括两个阶段:一阶核心微分CRN和二阶核心微分CRN,其中二阶导数计算是在一阶导数计算结果的基础上进行二次求导得到的。
以基于膜扩散原理的一阶核心导数CRN过程为例,由一个输入、两个输出和一个中间物种组成。输入的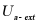 在膜外,且大量存在,以至于其浓度不受动力学的影响,一旦它穿过膜,就被标记为
在膜外,且大量存在,以至于其浓度不受动力学的影响,一旦它穿过膜,就被标记为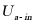 。物质
。物质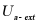 激活物质
激活物质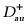 ,物质
,物质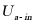 激活物质
激活物质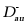 。最后,一个快速湮灭反应消除了
。最后,一个快速湮灭反应消除了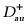 和
和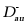 。此外,该论文详细阐述了如何基于除法运算和化学反应网络原理,求解组合项(或称复合项)的偏导数。
。此外,该论文详细阐述了如何基于除法运算和化学反应网络原理,求解组合项(或称复合项)的偏导数。
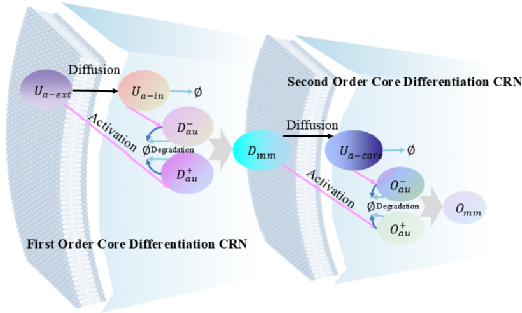
图3:基于膜扩散思想的偏微分求导CRN框图
4 基于CRNs的目标函数验证模块
图5描绘了基于目标函数验证模块的增广矩阵神经网络求解偏微分方程的架构图。值得注意的是,增设函数验证模块存在两个优势:一是用于刻画神经网络函数学习过程,动态计算目标函数的实时结果,即图5中的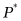 ;二是计算神经网络输出结果与目标函数的预期结果之间的误差值,即图5中的
;二是计算神经网络输出结果与目标函数的预期结果之间的误差值,即图5中的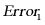 。
。
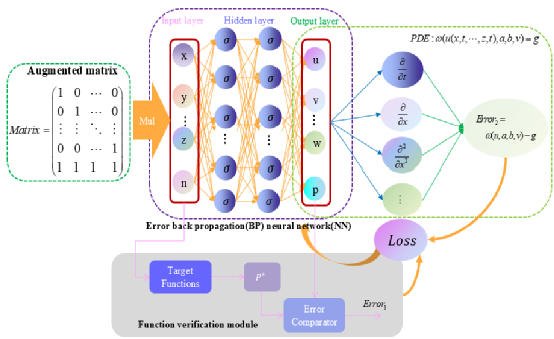
图4: 基于函数验证模块的增广矩阵神经网络求解偏微分方程
基于CRNs的函数验证模块的增广矩阵神经网络求解生物布鲁塞尔偏微分方程
Brusselator模型是研究非线性化学系统耗散结构和研究生物模式形成的经典理论模型。基于CRNs的Brusselator模型可表示为
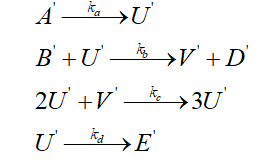
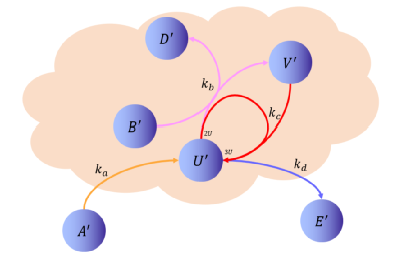
图5: 生物Brusselator反应模型架构
假设物质A和B的浓度均为常数,一维域上描述中间物种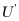 和
和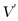 随时间和空间的浓度变化以及包含扩散项的微分方程可以表示为:
随时间和空间的浓度变化以及包含扩散项的微分方程可以表示为:
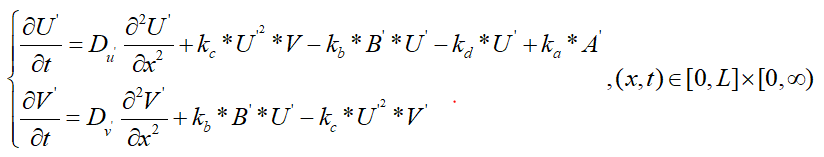
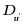 和
和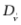 分别为
分别为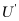 和
和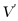 的扩散系数,
的扩散系数,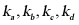
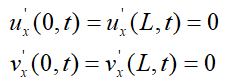
非负初始条件:
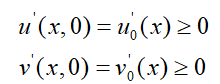
Brusselator反应-扩散系统(RD,Reaction-diffusion)没有已知的解析解,必须用数值方法进行求解。在没有扩散的情况下,若公式(65)实现稳态解,参数(a,b)需要满足:
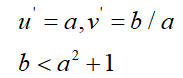
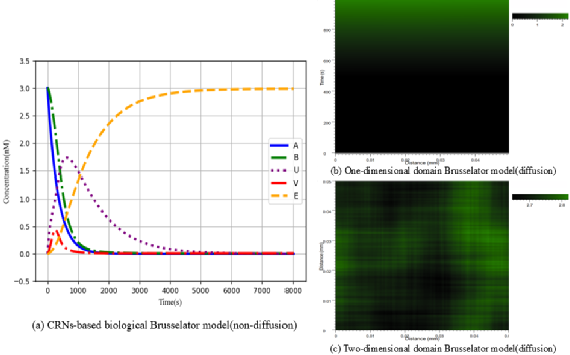
图6: 生物布鲁塞尔模型仿真结果
明显的, Brusselator RD系统主要涉及微分计算、二阶偏导数计算、加法运算、减法运算等。为简化偏微分方程求解过程,在研究过程中选择第一个方程作为研究对象。全文的研究主线,即基于提出的基于增广矩阵的反向传播神经网络和偏微分计算理论,实现偏微分方程求解。
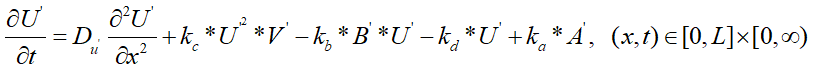
假设参数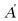 、
、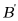 、
、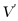 为常数,参量
为常数,参量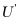 是关于
是关于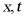 的函数,即
的函数,即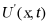 ,同时也是基于增广矩阵的反向传播神经网络的输出结果。上述公式可重写为:
,同时也是基于增广矩阵的反向传播神经网络的输出结果。上述公式可重写为:
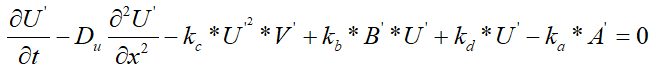
参考资料
Xiao, Yijun, Alfonso Rodríguez‐Patón, Jianmin Wang, Pan Zheng, Tongmao Ma, and Tao Song. "Programmable DNA‐Based Molecular Neural Network Biocomputing Circuits for Solving Partial Differential Equations." Advanced Science (2025): e07060.
内容中包含的图片若涉及版权问题,请及时与我们联系删除



评论
沙发等你来抢