机器学习算法的样本复杂度(sample complexity)表示成功学习目标函数所需的训练样本数。更准确地说,样本复杂度是开发者需要提供给算法的训练样本的数量,以使算法返回的函数在最佳函数的任意小误差范围内,并且概率任意接近1。样本复杂度有两种变体:弱变量固定特定的输入-输出分布。强变量采用所有输入-输出分布中最差情况的样本复杂性。
根据AMiner-NeurIPS 2020词云图和论文可以看出,与sample complexity是在本次会议中的热点,下面我们一起看看sample complexity主题的相关论文。

1.论文名称:Planning in Markov Decision Processes with Gap-Dependent Sample Complexity
论文链接:https://www.aminer.cn/pub/5ee3526a91e011cb3bff73ff?conf=neurips2020
简介:我们提出MDP-GapE,这是一种新的基于轨迹的蒙特卡洛树搜索算法,用于在马尔可夫决策过程中进行规划,其中对过渡具有有限的支持。 我们证明了对MDP-GapE识别高概率接近最优动作所需的生成模型的调用次数的上限。 这个与问题相关的样本复杂性结果用探索过程中访问的状态-动作对的次优差距表示。 我们的实验表明,与其他在固定置信度设置中具有样本复杂性保证的算法相反,MDP-GapE在实践中也很有效,而这些算法大多是理论上的。

2.论文名称:Sample Complexity of Uniform Convergence for Multicalibration
论文链接:https://www.aminer.cn/pub/5eb3dc4191e011ce31f27f31?conf=neurips2020
简介:人们越来越关注机器学习系统中的社会问题,尤其是在公平方面。多重校准提供了解决组公平性的综合方法。在这项工作中,我们解决了多重校准误差,并将其与预测误差解耦。使公平性度量标准(多重校准)与准确性(预测误差)脱钩的重要性在于两者之间固有的权衡,以及有关“正确权衡”的社会决策(监管机构多次强加)。我们的工作为多重校准误差的统一收敛保证提供了样本复杂性界限,这意味着无论准确度如何,我们都可以保证经验和(真实)多重校准误差相近。我们强调我们的结果:(1)比以前的界限更笼统,因为它们适用于不可知论和可实现的设置,并且不依赖于特定类型的算法(例如递归私有),(2)比以前的多重校准更好样本复杂度界限和(3)暗示了经典校准误差的一致收敛保证。
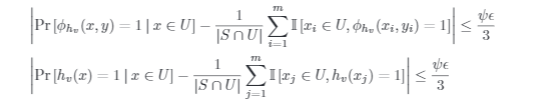
3.论文名称:Estimating decision tree learnability with polylogarithmic sample complexity
论文链接:https://www.aminer.cn/pub/5f7fdd328de39f0828397e8a?conf=neurips2020
简介:我们表明自上而下的决策树学习启发式方法适合于高效的可学习性估计:对于单调目标函数,这些启发式方法构造的决策树假设的误差可以通过多对数估计的多个带标签的示例进行估计,其指数小于运行这些启发式方法,并且实际上比学习一个好的决策树所需的信息理论最小值小得多。这增加了少量但不断增长的基础学习算法列表,这些算法已被证明适合于可学习性估计。在得出此结果的过程中,我们设计并分析了自上而下的决策树学习启发式方法的样本有效迷你批处理版本,并表明它们获得了与完整批处理版本相同的可证明保证。我们进一步给出这些启发式的“活动本地”版本:给定一个测试点x^ star,我们展示如何用多对数方法来计算决策树假设T的标签x^star许多带有标签的示例,其数量比学习T所需的数量小得多。

4.论文名称:Sample complexity and effective dimension for regression on manifolds
论文链接:https://www.aminer.cn/pub/5ee8986891e011e66831c35b?conf=neurips2020
简介:我们考虑使用重现内核希尔伯特空间方法对流形进行回归的理论。 流形模型出现在各种各样的现代机器学习问题中,我们的目标是帮助理解利用流形结构的各种隐式和显式降维方法的有效性。 我们的第一个主要贡献是根据微分几何建立Weyl定律的一种新的非渐近形式。 由此可见,流形上的光滑函数的某些空间实际上是有限维的,其复杂度根据流形维数而不是任何环境数据维来缩放。 最后,我们显示给定的(可能有噪声的)函数值在流形上随机地均匀地获取,核回归估计量(从流形的频谱分解中得出)产生由有效维数控制的误差范围。

5.论文名称:Revisiting the Sample Complexity of Sparse Spectrum Approximation of Gaussian Processes
论文链接:https://www.aminer.cn/pub/5f7fdd328de39f0828397ec0?conf=neurips2020
简介:我们为高斯过程引入了一种新的可伸缩近似,它具有可证明的保证,同时可在其整个参数空间上保持有效。 我们的近似值是通过对稀疏频谱高斯过程(SSGP)进行改进的样本复杂度分析获得的。 特别是,我们的分析表明,在一定的数据分解条件下,SSGP的预测和模型证据(用于训练)可以很好地近似具有较低样本复杂度的完整GP的预测和模型证据。 我们还开发了一种新的自动编码算法,该算法可找到一个潜在空间,以将潜在输入坐标分解为良好分隔的聚类,这适合我们的样本复杂度分析。 我们在几个基准上验证了我们提出的方法,并为我们的理论分析提供了有希望的结果。

内容中包含的图片若涉及版权问题,请及时与我们联系删除



评论
沙发等你来抢