ICML 2025 | k-Center问题——基于数据约简的高效近似算法

关键词：k-Center；欧式空间

导读

本文是 ICML 2025 会议接收论文 Faster Approximation Algorithms for k-Center via Data Reduction 的解读。该工作由北京大学姜少峰课题组与 Bar-Ilan University 的 Arnold Filtser、Nanyang Technological University 的 Yi Li、University of Bonn 的 Anurag Murty Naredla、Athena Research Center 的 Ioannis Psarros、Indiana University Bloomington 的 Qin Zhang 合作完成，论文主要贡献者之一杨乔媛为北京大学计算机学院博士生。

本研究针对欧式空间中的 k-Center 问题，提出高效的数据约简方法。在 k 较大的场景下，该方法首次实现了近线性时间的常数近似算法，在理论与实践层面提升了高维数据的聚类效率。

← 扫码跳转论文

论文地址：https://arxiv.org/abs/2502.05888

问题及背景

$k$ -Center 是一个经典聚类问题。给定欧式空间中的一个包含 $n$ 个点的集合 $P \subset \mathbb{R}^d$ 和一个整数 $k$ ， $k$ -Center 问题的目标是找到 $k$ 个中心点 $C\subset \mathbb{R}^d$ （ $|C|=k$ ），使得所有数据点到其最近中心的最大距离最小化。形式化地，优化目标为： $\mathrm{cost}(P,C):=\max_{p\in P} \text{dist}(p,C),$ 其中， $\text{dist}(p,q):=\lVert p-q\rVert_2$ 表示点 $p$ 和 $q$ 之间的欧式距离，而 $\text{dist}(p,C):=\min_{c\in C}\text{dist}(p,c)$ 表示点 $p$ 到集合 $C$ 的最短距离。该问题在常数维度（ $d=O(1)$ ）下已被证明是 APX‑hard；本文重点关注高维数据和大参数规模 $k$ （ $k=n^c$ ，其中 $0\lt c\lt 1$ ）下的高效算法设计。经典的 2-近似算法（如 Gonzalez 算法^[1]）在该设定下的时间复杂度为 $O(nkd)$ ，对于高维和大 $k$ 情况，这一复杂度过高。因此，设计更高效的近似算法具有重要的理论和实践意义。

核心思路

我们提出了一种基于数据约简（data reduction）的高效算法框架，其核心思想是构建 $\alpha$ -coreset。具体而言：

给定数据集 $P\subset \mathbb{R}^d$ ，我们构造其子集 $S \subset P$ 为 $\alpha$ -coreset，它具有以下关键性质：对于在 $S$ 上获得的任何 $\beta$ -近似解，都可以直接转化为原问题 $P$ 上的 $(\alpha + \beta)$ -近似解。通过首先构建满足 $|S|\ll|P|$ 的 $\alpha$ -coreset $S$ ，然后在 $S$ 上运行现有的 $\beta$ -近似算法，最终我们可以高效地获得原问题的 $(\alpha+\beta)$ -近似解。

该方法将计算复杂度从依赖全量数据规模 $|P|$ 降低为仅依赖 coreset 规模 $|S|$ ，非常适用于 $k=n^c$ （ $0\lt c\lt 1$ ）的大规模场景。

理论结果

针对欧式空间中的 $k$ -Center 问题，我们提出了两种 $\alpha$ -coreset 构造方法。

一、对于任意 $\alpha \ge 1$ ，可以在 $\tilde{O}(n)$ 时间内构建规模为 $\tilde{O}(kn^{1/\alpha^{2/3}})$ 的 coreset，以至少 $99\%$ 的成功概率保证获得 $O(\alpha)$ -近似解。

二、对于任意 $\alpha \ge 1$ ，可以在 $\tilde{O}(nk^{1/\alpha^2})$ 时间内构建规模为 $k\cdot \text{ploylog}(n)$ 的 coreset，同样保证 $O(\alpha)$ -近似解和 $99\%$ 的成功概率。

我们提出的两种 coreset 构建方法将欧式空间中的 $k$ -Center 问题的输入规模从 $n$ 降低到 $k\cdot o(n)$ 量级。这使得与现有的近似算法^[2]相结合时，首次在大规模 $k$ 设定下实现了 $O(1)$ -近似的近线性时间复杂度算法。

技术概述

对于结果一，我们设计了一种基于哈希函数的 coreset 构建方法。其核心是通过定义哈希映射函数 $\varphi:\mathbb{R}^d \to \mathbb{R}^d$ ，将原始数据集 $P\subset \mathbb{R}^d$ 中的每个点 $x$ 映射到特定的桶中。该哈希函数应确保每个桶的直径不超过 $\alpha \cdot \text{OPT}$ （其中 $\text{OPT}$ 表示 $k$ -Center 问题最优解的值），同时生成的哈希桶数量上界为 $\tilde{O}(kn^{1/\alpha^{2/3}})$ 。最终，我们从每个桶中选取一个代表点组成 coreset。

我们采用了一致性哈希（consistent hashing）^[3,4,5]作为技术基础，该技术能确保邻近点被映射到有限的哈希桶中。具体而言，我们基于随机平移网格（randomly-shifted grid）构造了新的哈希函数，并满足 $(\Gamma,\Lambda, \ell)$ -一致性哈希的定义要求：将 $\mathbb{R}^d$ 划分为直径上界为 $\ell$ 的哈希桶，并保证对任意直径不超过 $\ell/\Gamma$ 的点集，其跨桶数量的期望值不超过 $\Lambda$ 。我们提出的哈希函数首次实现了在 $\Gamma=\alpha$ （ $\alpha \gt 1$ ）时， $\Lambda=\exp(O(d/\alpha^c))$ （ $0\lt c \le 1$ ）的优异参数权衡，同时保持 $O(d)$ 的时间复杂度。这一成果显著改进了现有的一致性哈希技术，为 coreset 构造提供了高效的划分工具。

对于结果二，我们提出了一种基于随机命中集（random hitting sets）的 coreset 构造方法，采用多轮迭代采样策略构建 coreset。该方法通过 $O(\log (n))$ 轮迭代过程，每轮从数据集 $P$ 中均匀采样 $O(k\log n)$ 个点构成候选集，并利用 $\beta$ -近似最近邻查询（ $\beta$ -ANN）筛选出可被当前候选集充分代表（距离不超过 $2\beta\text{OPT}$ ）的数据点从 $P$ 中剔除。经过多轮迭代采样，最终由各轮候选集合共同组成规模为 $k\cdot \text{polylog}(n)$ 的 coreset。

实验验证

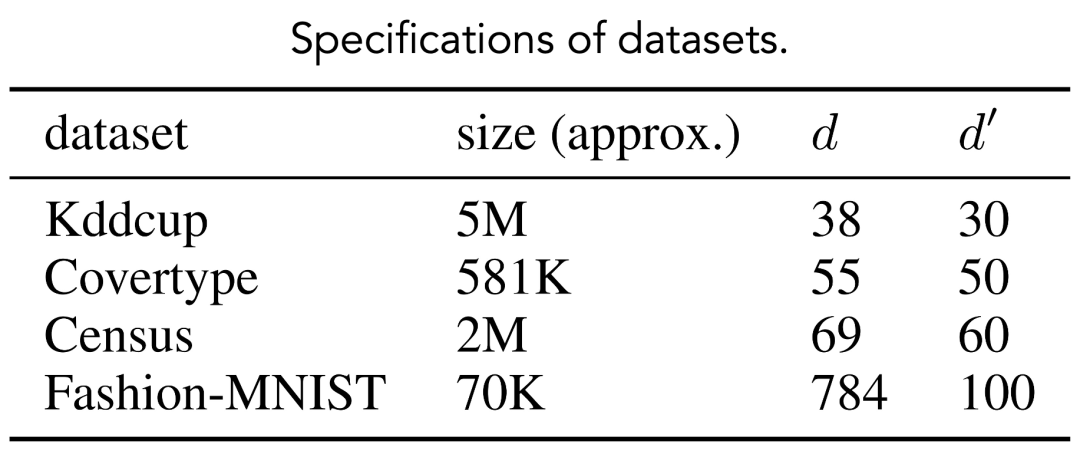
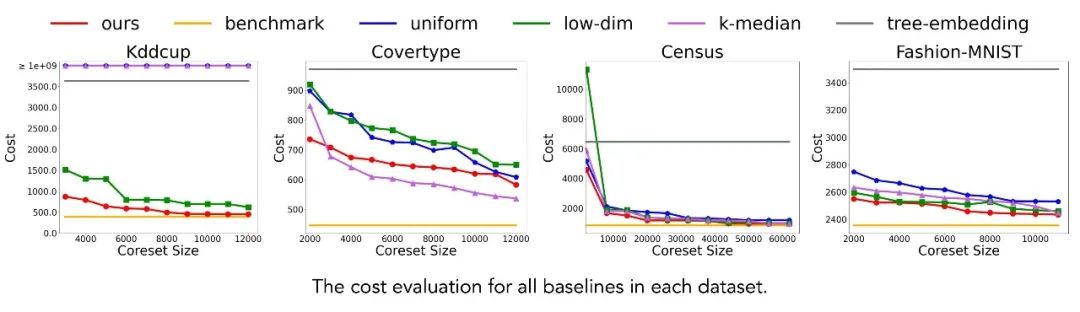
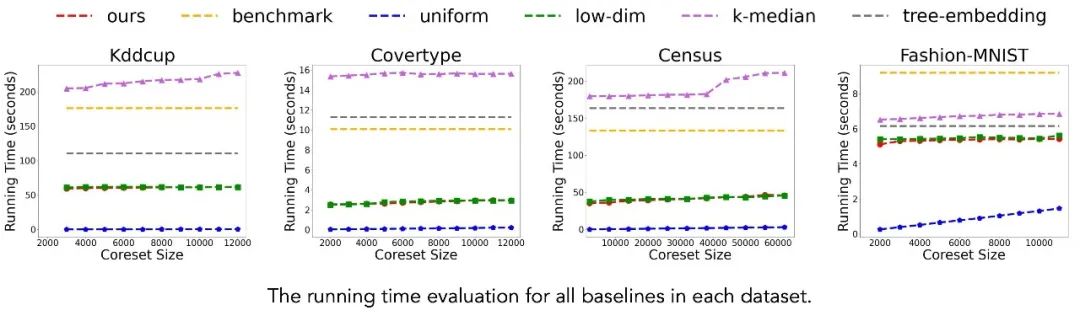
我们采用四个真实数据集进行实验验证，涵盖不同规模与维度特性。如表所示，各数据集的原始维度 $d$ 经Johnson-Lindenstrauss变换^[6]降维后得到目标维度 $d'$ 。

实验结果表明，本文提出的方法（ours）在所有数据集上均展现出显著优势。相比传统 Gonzalez 算法（benchmark），我们的方法在仅使用相对于原始数据集5%数据规模的 coreset 时，即可将聚类代价控制在基准方法的1.3倍以内，同时实现2-4倍的运行速度提升。

参考文献

[1] Gonzalez, T. F. Clustering to minimize the maximum intercluster distance. Theor. Comput. Sci., 38:293–306, 1985.
[2] Eppstein, D., Har-Peled, S., and Sidiropoulos, A. Approximate greedy clustering and distance selection for graph metrics. J. Comput. Geom., 11(1):629–652, 2020.
[3] Czumaj, A., Filtser, A., Jiang, S. H., Krauthgamer, R., Veselý, P., and Yang, M. Streaming facility location in high dimension via new geometric hashing. CoRR, abs/2204.02095, 2023. URL https://doi.org/10.48550/arXiv.2204.02095. see also conference version in FOCS22.
[4] Filtser, A. Scattering and sparse partitions, and their applications. ACM Trans. Algorithms, 20(4):30:1–30:42, 2024. See also conference version in ICALP20.
[5] Jia, L., Lin, G., Noubir, G., Rajaraman, R., and Sundaram, R. Universal approximations for tsp, steiner tree, and set cover. In STOC, pp. 386–395. ACM, 2005.
[6] Johnson, W. and Lindenstrauss, J. Extensions of Lipschitz maps into a Hilbert space. Contemporary Mathematics, 26:189–206, 01 1984.

图文 | 杨乔媛

PKU 姜少峰Lab

姜少峰博士，现任北京大学前沿计算研究中心助理教授、北京大学博雅青年学者，于2021年正式加入中心。他于2017年在香港大学获得博士学位，曾在以色列魏茨曼科学研究学院进行博士后研究，并曾在芬兰阿尔托大学任助理教授。他的研究方向为理论计算机科学，近期侧重于大数据算法及其在机器学习中的应用，并已在包括 STOC，FOCS，SICOMP，SODA，ICML，NeurIPS 等主流国际期刊和会议上发表论文多篇。

姜少峰Lab相关科研动态

本微信公众号所有内容，由北京大学前沿计算研究中心微信自身创作、收集的文字、图片和音视频资料，版权属北京大学前沿计算研究中心微信所有；从公开渠道收集、整理及授权转载的文字、图片和音视频资料，版权属原作者。本公众号内容原作者如不愿意在本号刊登内容，请及时通知本号，予以删除。

点“阅读原文”转论文链接

内容中包含的图片若涉及版权问题，请及时与我们联系删除

ICML 2025 | k-Center问题——基于数据约简的高效近似算法

评论