自注意力机制的“思维切换”：从位置记忆到语义理解的相变

摘要

众多实证研究已经发现，随着训练规模和数据量的增加，大语言模型中会自发涌现出不同的算法机制，从而显著提升模型的能力。然而，目前缺乏对这些机制如何产生的理论性刻画。本文在可解的点积注意力（dot-product attention）模型中，通过对具有可训练、低秩查询（query）与键（key）矩阵的非线性交互层进行严格的高维分析，给出了经验风险最小化（empirical risk minimization）非凸损失全局最优解的闭式特征化。研究表明，该最优解对应于两种截然不同的注意力机制：一种是“基于位置”的注意力（positional attention），即标记（token）根据其在序列中的位置相互作用；另一种是“基于语义”的注意力（semantic attention），即标记根据其语义内容相互作用。更重要的是，随着样本复杂度（sample complexity）的提升，模型会在这两种机制之间发生清晰的相变（phase transition）。最后，我们将点积注意力与只能实现位置机制的线性位置基线模型进行比较，验证在数据量充足时点积注意力凭借语义机制能够显著优于线性基线。

如果你对这一主题感兴趣，这周「大模型可解释性」读书会会带我们从神经科学的视角理解大模型的认知机制，欢迎你来参与！

关键词：点积注意力（dot-product attention），位置注意（positional attention），语义注意（semantic attention），样本复杂度（sample complexity），高维极限（high-dimensional limit），相变（phase transition）

彭晨丨作者

赵思怡丨审校

论文题目：A phase transition between positional and semantic learning in a solvable model of dot-product attention

论文链接：https://arxiv.org/abs/2402.03902

发表时间：2024年10月

论文来源：NeurIPS 2024

近年来，自注意力（self-attention）层成为从文本数据中抽取信息的核心结构，既能捕捉单词顺序暗含的位置信息，同时也能借助词嵌入理解单词语义。大量实验揭示，训练过程和数据量会决定注意力层究竟采用何种算法机制，但缺乏理论依据。受物理学中“相变”理论启发，本文构建了一个可解析、只含单层点积注意力的师生模型，并在高维极限下通过精确计算证明，模型会在“位置”与“语义”两种注意力机制之间发生清晰的相变，为神经网络中算法机制的涌现提供了首个严格理论刻画。

注意力层会发生涌现吗？

注意力层最早被提出用于并行处理序列数据，其核心思想是为序列中每对标记计算相似度得分，进而加权融合信息。在实践中，研究者通过对训练好的大规模语言模型进行机理可解释性（mechanistic interpretability）分析，发现注意力层能够实现多种算法——有时侧重于位置编码（positional attention），有时依赖于词向量之间的语义相似度（semantic attention）。这些机制的具体形成不仅与网络结构和训练算法相关，还与可获得的数据量密切挂钩。然而，就像物理学家在研究铁磁材料时提出的相变（phase transition）概念一样，人们尚不清楚在注意力层中，随着样本规模增长，那些定量指标会否出现突变，从而使得模型在位置与语义机制之间发生切换。本文正是在这样的背景下，借鉴统计物理中处理大规模粒子系统的方法，为注意力层的机制涌现提供理论支撑。

模型构建：可解的低秩点积注意力范式

为获得可解析的理论结果，研究者设计了一个简化的自注意力模型，仅包含一层点积注意力（dot-product attention），并对查询与键使用同一可训练矩阵，即共享权重（tied weights），且限制为低秩结构。基于理论机器学习常用的师生框架，“教师”注意力矩阵由内置的“位置机制”（positional component）和“语义机制”（semantic component）叠加而成，这保证了数据既包含清晰的位置依赖，也包含深层的语义关联。而“学生”模型在师生框架下，通过经验风险最小化在高维极限求解， 从带有位置编码（positional encodings）的输入中学习一种线性映射，从而逼近教师的混合注意力矩阵。该映射在数学上对应于最小化带 ℓ₂ 正则化的均方误差损失。

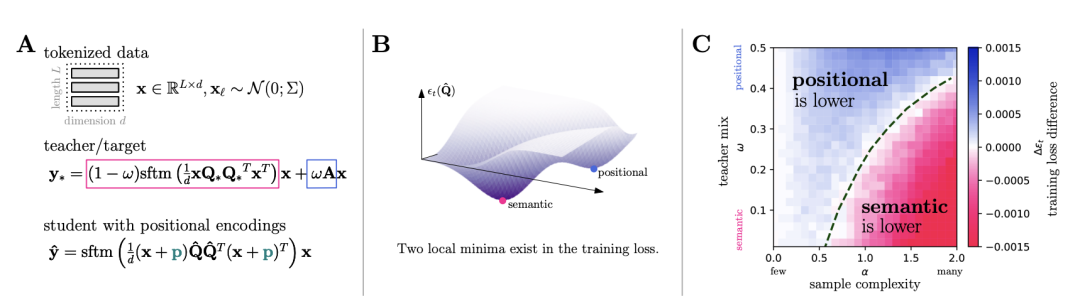
图 1. 注意力简化模型中的相变。(A)我们在师生环境中研究了一个关联的低秩注意模型。教师根据语义（作为标记内容x的函数）和位置（作为标记位置的函数）注意力矩阵，混合d维的L个单独令牌。学生只能使用位置编码p来拟合老师的位置属性。(B)教师损失景观的示意图，其中包含位置最小值和语义最小值。(C)我们发现，在渐近高维极限下，作为样本复杂性和教师组成的函数，全局最小值切换，构成了位置学习和语义学习之间的相变。

高维极限下的闭式特征化

在输入维度 d 与样本数量 n 同比增大、样本复杂度 α = n/d 保持常数的高维极限中，研究者运用广义近似消息传递（Generalized Approximate Message Passing, GAMP）算法的状态演化理论，以及对应的自洽方程，给出了训练损失与测试误差在最优解处的闭式表达。

GAMP：一种对高维贝叶斯估计或经验风险最小化问题能达到信息论最优的迭代方法

核心思想是，将高维的非凸优化问题“压缩”为若干维度固定的统计量求解，通过解这套自洽方程，即可直接判断全局最优解对应的位置／语义机制，并准确计算常数级误差值。该理论不仅展现出与有限维实验结果的高度一致性，还能预测不同样本复杂度下最优解的定性变化。

位置—语义表征相变

基于闭式特征化，研究者进一步考察了随样本复杂度 α 增长而发生的全局最优解切换现象。在“语义权重”较低的任务中，当 α 小于临界值 α_c 时，全局最优解对应的学生模型只利用位置编码实现注意力；但一旦 α 超过  α_c ，学生模型便会忽略位置编码，转而通过学习查询和键矩阵与教师语义权重的重叠，实现基于语义的注意力。这一现象与物理学中亚临界与超临界相变高度类比，体现了注意力层在算法机制层面上的“突变式”行为。

为了凸显语义机制的重要性，研究者将点积注意力模型与只能实现位置混合的全连接线性基线模型做了对比。结果显示，在样本复杂度低于 α_l时，纯位置基线反而略优于点积注意力；但在 α > α_l 区间，点积注意力凭借其学习到的语义机制，测试误差显著低于线性基线。这进一步说明，当数据量充足时，只有具备捕捉输入向量内在语义结构能力的注意力架构，才能发挥其优势。

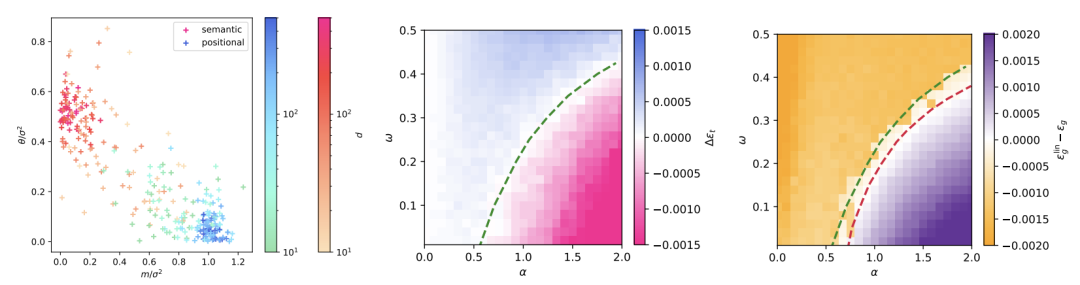
图 2. 语义和位置训练损失之间的相变。（左）对于α = 1.5，同时缩放 d 和 n 时，θ 和 m 在不同位置分别收敛于位置局部极小值和语义局部极小值。（中）颜色图表示使用 Pytorch 实现的全批量梯度下降训练模型时，在 p1 或 Q⋆ 处初始化分别收敛时训练损失的差异。绿色虚线表示理论预测的阈值 α_c(ω)，超过该阈值时，语义解的损失低于位置解的损失。（右）颜色图表示使用 Pytorch 实现的全批量梯度下降训练注意力模型（13）时，在 Q⋆ 处初始化和密集线性基线在收敛时测试均方误差的差异。红色虚线表示理论预测的阈值样本复杂度α_l(ω)，超过该阈值时，点积注意力优于基线。

结论与展望

本文首次从严格的高维概率角度，为点积注意力层中位置与语义算法机制的涌现提供了闭式理论刻画，并揭示了两者之间的相变现象。这一发现不仅加深了我们对注意力机制本质的理解，也为设计和调优具有更好泛化能力的自注意力模型提供了新思路。

后续研究可在以下方向拓展：引入多头（multi-head）与跨注意力（cross-attention）结构；将模型应用于更贴近实际的非高斯、长序列场景；以及分析随机初始化和梯度下降算法在此损失景观中的轨迹与收敛性，以期全面理解从“随机猜测”到“全局最优”的动态过程。

-直播预告-

大模型可解释性读书会

集智俱乐部联合上海交通大学副教授张拳石、阿里云大模型可解释性团队负责人沈旭、彩云科技首席科学家肖达、北京师范大学硕士生杨明哲和浙江大学博士生姚云志共同发起「大模型可解释性」读书会。本读书会旨在突破大模型“黑箱”困境，尝试从以下四个视角梳理大语言模型可解释性的科学方法论：

自下而上：Transformer circuit 为什么有效？

自上而下：神经网络的精细决策逻辑和性能根因是否可以被严谨、清晰地解释清楚？

复杂科学：渗流相变、涌现、自组织等复杂科学理论如何理解大模型的推理与学习能力？

系统工程：如何拥抱不确定性，在具体的业界实践中创造价值？

五位发起人老师会带领大家研读领域前沿论文，现诚邀对此话题感兴趣的朋友，一起共创、共建、共享「大模型可解释性」主题社区，通过互相的交流与碰撞，促进我们更深入的理解以上问题。无论您是致力于突破AI可解释性理论瓶颈的研究者，探索复杂系统与智能本质的交叉学科探索者，还是追求模型安全可信的工程实践者，诚邀您共同参与这场揭开大模型“黑箱”的思想盛宴。

读书会已于2025年6月19日启动，每周四晚19:30-21:30，预计持续分享8-10周左右。

详情请见：破解AI黑箱的四重视角：大模型可解释性读书会启动

6. 高考分数只是张入场券，你的科研冒险在这里启航！

7. 系统科学前沿十讲：理解自然、生命与社会的复杂性