从神经动力学到意识：跨尺度计算、演化与涌现丨计算神经科学第三季·读书会启动

导语

从单个神经元的放电到全脑范围的意识涌现，理解智能的本质与演化始终是一个关于尺度的问题。更值得深思的是，无论是微观的突触可塑性、介观的皮层模块自组织，还是宏观的全局信息广播，不同尺度的动力学过程都在共同塑造着认知与意识。这说明，对心智的研究从最初就必须直面一个核心挑战：局部的神经活动如何整合为统一的体验？局域的网络连接又如何支撑灵活的智能行为？

继「神经动力学模型」与「计算神经科学」读书会后，集智俱乐部联合来自数学、物理学、生物学、神经科学和计算机的一线研究者共同发起「从神经动力学到意识：跨尺度计算、演化与涌现」读书会，跨越微观、介观与宏观的视角，探索意识与智能的跨尺度计算、演化与涌现。重点探讨物理规律与人工智能如何帮助我们认识神经动力学，以及神经活动跨尺度的计算与演化如何构建微观与宏观、结构与功能之间的桥梁。

读书会背景

传统神经科学往往聚焦于特定尺度——或是分子机制，或是脑区功能。但现代研究正在打破这种分野。当重尾网络揭示神经编码的新规律，当发育中的皮层自发形成跨物种的通用结构，当多脑区协同涌现出意识状态时，我们不得不重新思考：智能是特定尺度的专属现象，还是所有层次共同作用的结果？不同尺度的过程如何相互约束、相互促进？这些追问正在重塑我们对大脑和心智的理解。

读书会简介

本次读书会我们将探讨神经元如何通过重尾连接产生临界雪崩和低维混沌等非线性动力学，揭示局部神经环路中的异质性如何增强神经网络的信息处理能力；视皮层自组织、多脑区发育等过程，分析神经模块（Modular Structure）如何通过图灵不稳定性形成功能特化结构，探索进化保守性与环境适应性之间的张力；AI 驱动的脑建模如何帮助我们建立连接神经机制与认知功能的跨尺度理论框架；全脑信息整合如何连接微观放电模式与宏观意识状态，构建解释层级间相互作用的数学语言。

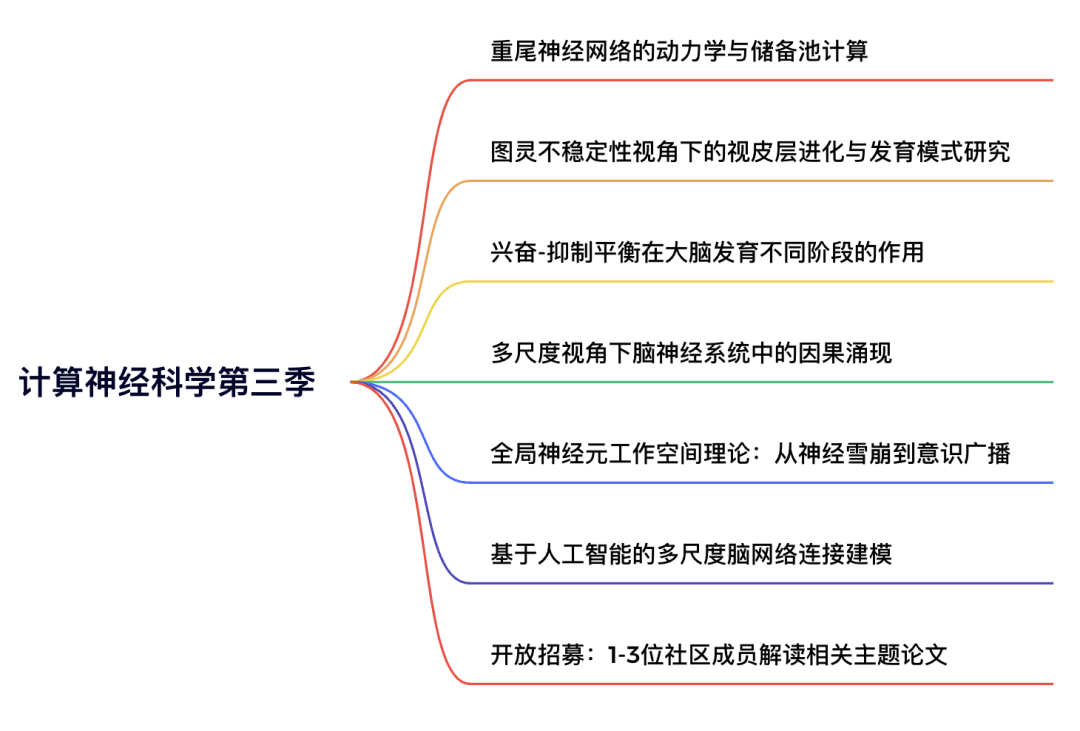
读书会框架

发起人团队

杨骏，佐治亚理工学院（Georgia Tech）定量生物学在读博士，本科毕业于清华大学，获得了数理基础科学 + 电气工程双学士学位。本科时曾师从 Sukbin Lim 和 Mayank Mehta 研究神经科学。在Audrey Sederberg的实验室完成短暂轮转后，现在正在 Hannah Choi 的实验室探索网络模体（motif）对动力学的影响。研究兴趣：神经编码理论与神经动力学。

邹立诚，马克斯普朗克动力学与自组织研究所博士生，师从神经物理学家Fred Wolf。本科就读于上海交通大学致远学院数学方向，于李松挺及周栋焯课题组取得学士学位。硕士毕业于荷兰阿姆斯特丹大学生物医学科学系，在读期间曾长期访问巴塞罗那国际数学研究中心及哥廷根灵长类动物研究所。 研究兴趣：记忆的表征与存储，突触动力学，皮层尺度的神经元动力学模拟，初级视皮层发育与进化的定量研究。

孔德玥，法兰克福高等研究院在读博士生，师从 Matthias Kaschube 教授。本科毕业于香港科技大学，获得计算机+细胞生物学学位，在胡禹老师课题组完成毕业论文。研究兴趣：神经环路的早期发育，神经动力学，光遗传对神经环路的扰动。

王志鹏，北京师范大学在读博士，师从张江教授，研究兴趣包括复杂系统多尺度建模、因果涌现等。

吴佳铭，巴黎萨克雷大学物理学博士，师从 Marcelo Rozenberg 教授，研究兴趣：固体物理、脑计算、神经网络动力学、具身智能等。

李宗晟，香港中文大学（深圳）在读博士，师从南方科技大学刘泉影教授，本科毕业于大连理工大学，硕士毕业于南洋理工大学。在广东省智能科学与技术研究院陈洛南老师的实验室完成科研助理的短暂轮转后，现聚焦于人工智能与神经计算方向。研究兴趣包括 AI 孪生脑建模，神经数据解码，情绪动力学等。

报名参与读书会

运行模式

从2025年9月20日开始，每周六晚上19:00-21:00，持续时间预计8周左右，按读书会框架设计，每周进行线上会议，与主讲人等社区成员当面交流，会后可以获得视频回放持续学习。

报名方式

第一步：微信扫码填写报名信息。

扫码报名（可开发票）

第二步：填写信息后，付费报名。如需用支付宝支付，请在PC端进入读书会页面报名支付：

https://pattern.swarma.org/study_group/69?from=wechat

第三步：添加运营负责人微信，拉入对应主题的读书会社区（微信群）。

PS：为确保专业性和讨论的聚焦，本读书会谢绝脱离读书会主题和复杂科学问题本身的空泛的哲学和思辨式讨论；如果出现讨论内容不符合要求、经提醒无效者，会被移除群聊并对未参与部分退费。

读书会运营负责人

加入社区后可以获得的资源：

完整权限，包括线上问答、录播回看、资料共享、社群交流、信息同步、共创任务获取积分等。

参与共创任务获取积分，共建学术社区：

读书会采用共学共研机制，成员通过内容共创获积分（字幕修改、读书会笔记、论文速递、公众号文章、集智百科、论文解读等共创任务），积分符合条件即可退费。

PS：具体参与方式可以加入读书会后查看对应的共创任务列表，领取任务，与运营负责人沟通详情，上述规则的最终解释权归集智俱乐部所有。

读书会阅读材料

阅读材料较长，为了更好的阅读体验，建议您前往集智斑图沉浸式阅读，并可收藏感兴趣的论文。

https://pattern.swarma.org/article/365

「从神经动力学到意识：跨尺度计算、演化与涌现」读书会阅读清单

主题一 重尾神经网络的动力学与储备池计算

召集人：杨骏

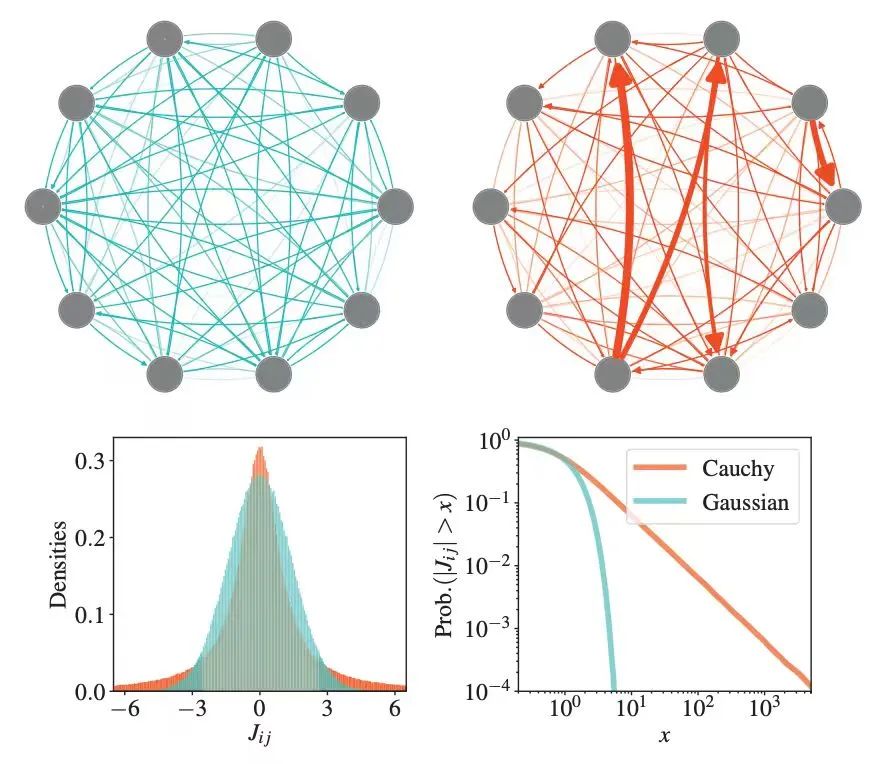
介绍：传统的RNN模型通常假设神经元之间具有强度服从高斯分布的全连接或者具有相同强度的稀疏连接。然而，实验和理论表明神经元之间的连接强度更接近重尾（heavy-tailed）分布。由于重尾分布的二阶矩通常发散，常规的分析理论如动力学平均场（dynamic mean-field）和扩散近似不再适用。所以，重尾神经网络的动力学与经典的高斯或稀疏均匀神经网络完全不同，将经典 RNN 理论推广到重尾 RNN 对连接理论与实验结果具有重要意义。在这一部分，我们将回顾关于重尾 RNN 动力学的文献，对比高斯网络和重尾网络的动力学，并讨论这些理论结果在神经科学背景下的意义和其他开放问题。

核心关注问题：

1. 重尾连接分布如何塑造神经网络的动力学和信息处理？

2. 重尾网络动力学是否与真实脑网络的动力学更接近？

3. 重尾神经网络在机器学习领域有什么潜在的应用？

核心文献：

这是第一篇讨论重尾神经网络性质的文献。这篇文章发现 Cauchy 连接 RNN 有类似神经元雪崩的临界行为。

1. Kuśmierz, Ł., S. Ogawa and T. Toyoizumi (2020). "Edge of Chaos and Avalanches in Neural Networks with Heavy-Tailed Synaptic Weight Distribution." Physical Review Letters125(2): 028101.

第一篇讨论重尾 SNN 的文献。将经典神经网络的 population density method 中的扩散近似推广到重尾神经网络的分数阶扩散近似。

2. Wardak, A. and P. Gong (2021). "Fractional diffusion theory of balanced heterogeneous neural networks." Physical Review Research3(1): 013083.

研究了一个纯抑制性的 lognormal 网络，并考虑了连接的对称性如何破坏遍历性（lognormal 的二阶矩有限）。

3. Berlemont, K. and G. Mongillo (2022). "Glassy phase in dynamically-balanced neuronal networks." bioRxiv: 2022.2003.2014.484348.

唯一一篇讨论连续时间重尾神经网络动力学的文章。给出了重尾随机矩阵的谱密度和 Lévy 平均场理论，发现了重尾神经网络动力学的多重分形结构，并讨论了局域化对于储备池计算（reservoir computing）的意义。

4. lWardak, A. and P. Gong (2022). "Extended Anderson Criticality in Heavy-Tailed Neural Networks." Physical Review Letters129(4): 048103.

推广到有限大的 Lévy α-stable 离散时间 RNN，详细讨论了动力学的维数问题。

5. Xie, Y., S. Mihalas and Ł. Kuśmierz (2025). "Slow Transition to Low-Dimensional Chaos in Heavy-Tailed Recurrent Neural Networks." arXiv. 将 Kuśmierz et al. (2020)

推荐阅读：

这篇文章使用了包含一种兴奋性神经元和 PV, SST, VIP 三种抑制性神经元的稀疏 lognormal SNN，但没有对该网络的详细动力学分析。

1. Guo, L. and A. Kumar (2023). "Role of interneuron subtypes in controlling trial-by-trial output variability in the neocortex." Communications Biology 6(1): 874.

发现在具有随距离 lognormal 分布的连接强度的 SNN 中存在一种次序传播。

2. Riquelme, J. L., M. Hemberger, G. Laurent and J. Gjorgjieva (2023). "Single spikes drive sequential propagation and routing of activity in a cortical network." eLife 12: e79928.

高斯神经网络的经典文献。给出了经典混沌 RNN 的 Lyapunov 谱。

3. Engelken, R., F. Wolf and L. F. Abbott (2023). "Lyapunov spectra of chaotic recurrent neural networks." Physical Review Research 5(4).

高斯神经网络的经典文献。讨论了连接的一阶和二阶统计量如何影响经典 RNN 的 participation ratio（PR）维数。

4. Clark, D. G., L. F. Abbott and A. Litwin-Kumar (2023). "Dimension of Activity in Random Neural Networks." Physical Review Letters 131(11): 118401.

联系了高斯 RNN 和稀疏均匀 RNN 的混沌相变，并讨论了 SNN 中的类似现象。

5. Kadmon, J. and H. Sompolinsky (2015). "Transition to Chaos in Random Neuronal Networks." Physical Review X 5(4).

高斯神经网络经典文献。讨论了混沌相的平衡点分布。

6. Stubenrauch, J., C. Keup, A. C. Kurth, M. Helias and A. van Meegen (2025). "Fixed point geometry in chaotic neural networks." Physical Review Research 7(2): 023203.

从理论上给出了从协方差分布区分混沌边缘和临界雪崩两种临界动力学的方法。

7. Dahmen, D., S. Grün, M. Diesmann and M. Helias (2019). "Second type of criticality in the brain uncovers rich multiple-neuron dynamics." Proceedings of the National Academy of Sciences 116(26): 13051-13060.

第一篇讨论 RNN 动力学局域化的文献。

8. Monteforte, M. and F. Wolf (2010). "Dynamical Entropy Production in Spiking Neuron Networks in the Balanced State." Physical Review Letters 105(26): 268104.

简单的可塑性规则如何产生重尾分布的连接。

9. Lynn, C., C. Holmes and S. Palmer (2024). "Heavy-tailed neuronal connectivity arises from Hebbian self-organization." Nature Physics 20: 1-8.

处理稀疏均匀 SNN 的经典方法。

10. Brunel, N. and V. Hakim (2022). Population density model. Encyclopedia of Computational Neuroscience. D. Jaeger and R. Jung, Springer, New York, NY: 2846-2865.

社区招募：

Morrell 模型通过引入若干个缓变隐变量可以产生类似于生物神经网络中观察到的临界雪崩。

1. Morrell, M. C., I. Nemenman and A. Sederberg (2024). "Neural criticality from effective latent variables." eLife 12: RP89337.

2. Morrell, M. C., A. J. Sederberg and I. Nemenman (2021). "Latent Dynamical Variables Produce Signatures of Spatiotemporal Criticality in Large Biological Systems." Physical Review Letters 126(11): 118302.

主题二 图灵不稳定性视角下的视皮层进化与发育模式研究

召集人：邹立诚

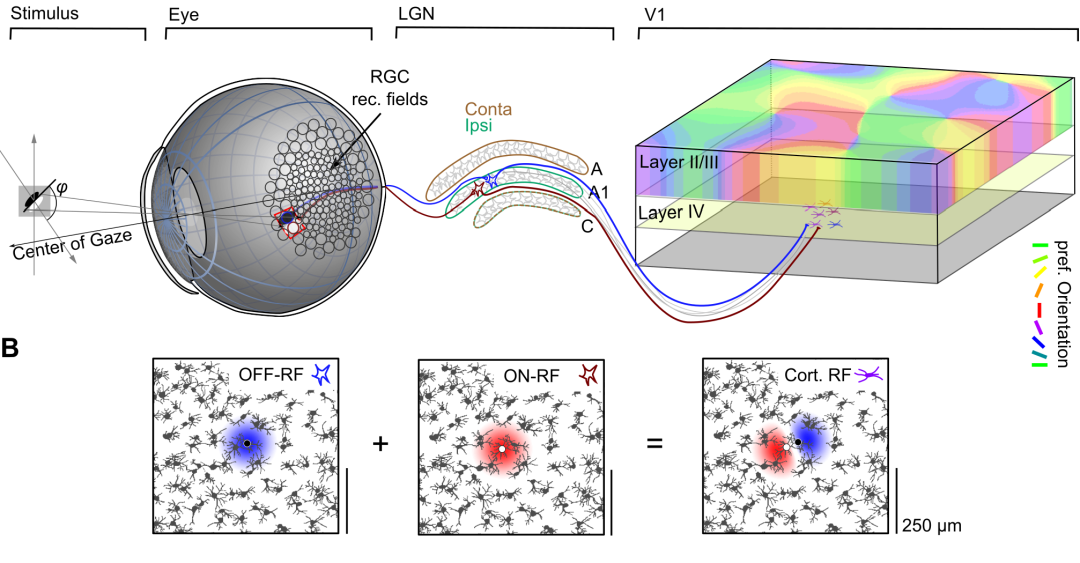
灵长类动物的初级视皮层（primary visual cortex，V1） 拥有大量对朝向展现选择性（orientation selective）的兴奋性神经元，这一经典的实验现象自50年代由诺奖得主 Hubel & Wiesel 汇报起便吸引了广泛的研究，直至今日已取得众多突破性认识。其中，非齿类大目动物（Non-Glires）成熟 V1 神经元群的偏好朝向在空间分布上呈垂直方向一致，水平方向似周期（quasi-periodic）变化的特点。该空间分布模式被称为 Orientation Preference Map（OPM），其形成的机制吸引了众多理论神经物理学家的兴趣。OPM 如何从刚出生时的 absence 到成熟时的 presence 可以用非平衡统计物理中的图灵不稳定性来定量描述，该模型预测了V1 OPM拥有奇异点密度（pinwheel density）为圆周率常数 π 的跨物种 common design, 并于2010年由 (Kaschube et al., 2010, Science) 分析光学成像数据证实。这一轰动性的成果推断该 common design 是视皮层进化的必然结果，其形成只依赖 V1 神经元在静息态的自组织（self-organization）而非此前长期认为的由视网膜和丘脑调控。在之后的15年间不同实验室对不同物种的视觉实验证明了该推断的可靠性。因此，如何用图灵不稳定性的自组织理论定量理解视皮层在进化与发育中的模式形成（pattern formation）是本期读书会所关心的话题，我们将从实验和理论两个方面并行出发，回顾针对 OPM common design 探索的历史长河中两者如何互相启发并一步步揭开其神秘面纱。

核心关注问题：

1. 如何用数学语言定量地描述初级视皮层跨物种的发育动力学？

2. 什么是朝向选择性，为什么关心初级视皮层神经元的朝向选择性？

3. 实验和理论如何相互启发与推动初级视皮层的研究？

核心文献：

介绍了为什么OPM的common design是进化的结果。

1. Schmidt, K. E., & Wolf, F. (2021). Punctuated evolution of visual cortical circuits? Evidence from the large rodent Dasyprocta leporina, and the tiny primate Microcebus murinus. Current opinion in neurobiology, 71, 110-118.

第一次在in-vivo论证了V1的发育是自组织。

2. Mulholland, H. N., Kaschube, M., & Smith, G. B. (2024). Self-organization of modular activity in immature cortical networks. Nature communications, 15(1), 4145.

轰动性成果，发现Π=visual cortex。

3. Kaschube, M., Schnabel, M., Löwel, S., Coppola, D. M., White, L. E., & Wolf, F. (2010). Universality in the evolution of orientation columns in the visual cortex. science, 330(6007), 1113-1116.

第一个也是唯一一个能定量拟合所有OPM统计学性质的模型

4. Wolf, F. (2005). Symmetry, multistability, and long-range interactions in brain development. Physical review letters, 95(20), 208701.

推荐阅读：

这篇文章很勇，直接否定了OPM的形成是由视网膜和丘脑决定的。

1. Smith, G. B., Hein, B., Whitney, D. E., Fitzpatrick, D., & Kaschube, M. (2018). Distributed network interactions and their emergence in developing neocortex. Nature neuroscience, 21(11), 1600-1608.

也顺便推荐一些反对V1 self-organization的文献，这几篇也是经典

2. Schottdorf, M., Keil, W., Coppola, D., White, L. E., & Wolf, F. (2015). Random wiring, ganglion cell mosaics, and the functional architecture of the visual cortex. PLoS computational biology, 11(11), e1004602.

3. Ferster, D., & Miller, K. D. (2000). Neural mechanisms of orientation selectivity in the visual cortex. Annual review of neuroscience, 23(1), 441-471.

4. Paik, S. B., & Ringach, D. L. (2011). Retinal origin of orientation maps in visual cortex. Nature neuroscience, 14(7), 919-925.

5. Najafian, S., Koch, E., Teh, K. L., Jin, J., Rahimi-Nasrabadi, H., Zaidi, Q., ... & Alonso, J. M. (2022). A theory of cortical map formation in the visual brain. Nature communications, 13(1), 2303.

这个模型在2025年来看确实错的离谱，但站在当时的角度确实是很前沿的理论。

6. Wolf, F., & Geisel, T. (1998). Spontaneous pinwheel annihilation during visual development. Nature, 395(6697), 73-78.

社区招募：

1. Fumarola, F., Hein, B., & Miller, K. D. (2022). Mechanisms for spontaneous symmetry breaking in developing visual cortex. Physical Review X, 12(3), 031024.

主题三 兴奋-抑制在大脑发育不同阶段的作用

召集人：孔德玥

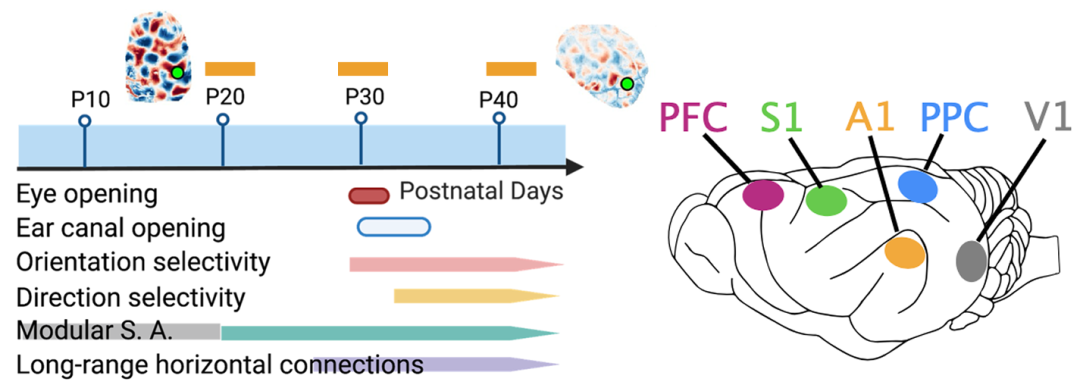
理解大脑如何从发育早期的相对均质状态逐渐分化形成功能高度特异化的成熟皮层区域（如处理感官信息的初级视皮层V1与负责复杂认知的前额叶皮层PFC），是神经科学的核心问题之一。传统理论主要关注不同脑区先天预置或后天经验驱动的独特组织模式。在本期读书会中，我们将聚焦大脑功能形成的三个关键方面：共享起点、协同演化，和情境驱动。具体而言，首先，早期共有的模块化网络为跨脑区提供了通用功能基础；继而，保守的发育程序结合区域特异性调整逐渐塑造了成熟脑区的结构差异；最终，在特定感觉或认知情境下，区域特异的动态计算机制（如V1的刺激强度依赖性切换机制）得以实现高效的信息处理。我们将特别探讨兴奋-抑制平衡如何在这三个阶段中发挥核心调控作用。

核心关注问题：

1. 发育过程中，大脑的神经活动，连接结构和功能经历了哪些变化？

2. 兴奋和抑制神经元群体群体活动如何调控大脑的发育过程？

3. 发育如何帮助大脑实现高效信息处理？

核心文献：

这篇讲的是早期发育中自发活动的空间结构

1. N.J. Powell, B. Hein, D. Kong, J. Elpelt, H.N. Mulholland, M. Kaschube, & G.B. Smith, Common modular architecture across diverse cortical areas in early development, Proc. Natl. Acad. Sci. U.S.A. 121 (11) e2313743121, https://doi.org/10.1073/pnas.2313743121 (2024).

展示了早期自发活动和特征选择性之间存在的关系

2. Smith, G. B., Hein, B., Whitney, D. E., Fitzpatrick, D., & Kaschube, M. (2018). Distributed network interactions and their emergence in developing neocortex. Nature neuroscience, 21(11), 1600-1608.

神经非线性如何实现情境相关调节

3. Rubin DB, Van Hooser SD, Miller KD. The stabilized supralinear network: a unifying circuit motif underlying multi-input integration in sensory cortex. Neuron. 2015 Jan 21;85(2):402-17. doi:10.1016/j.neuron.2014.12.026.

推荐阅读：

这篇主要讲发育过程中自发神经活动和视觉刺激导致的神经活动如何变得更相似，以及什么样的环路连接结构变化在这之中起作用

1. Trägenap, S., Whitney, D.E., Fitzpatrick, D. et al. The developmental emergence of reliable cortical representations. Nat Neurosci 28, 394–405 (2025). https://doi.org/10.1038/s41593-024-01857-3

基于小鼠的实验数据，这篇的作者们提出了比较完整的神经环路面对光遗传扰动的反应理论

2. Chau HY, Miller KD, Palmigiano A. Exact linear theory of perturbation response in a space- and feature-dependent cortical circuit model. bioRxiv [Preprint]. 2025 Jun 21:2024.12.27.630558. doi: 10.1101/2024.12.27.630558. PMID: 39896520; PMCID: PMC11785077.

开放招募：

这两篇都是关于光遗传扰动后神经环路反应的建模工作

1. O’Shea, Daniel J., Lea Duncker, Werapong Goo, Xulu Sun, Saurabh Vyas, Eric M. Trautmann, Ilka Diester, Charu Ramakrishnan, Karl Deisseroth, Maneesh Sahani, and Krishna V. Shenoy. 2022. ‘Direct Neural Perturbations Reveal a Dynamical Mechanism for Robust Computation’. 2022.12.16.520768.

2. Oldenburg IA, Hendricks WD, Handy G, Shamardani K, Bounds HA, Doiron B, Adesnik H. The logic of recurrent circuits in the primary visual cortex. Nat Neurosci. 2024 Jan;27(1):137-147. doi: 10.1038/s41593-023-01510-5. Epub 2024 Jan 3. PMID: 38172437; PMCID: PMC10774145.

主题四 多尺度视角下脑神经系统中的因果涌现

召集人：王志鹏

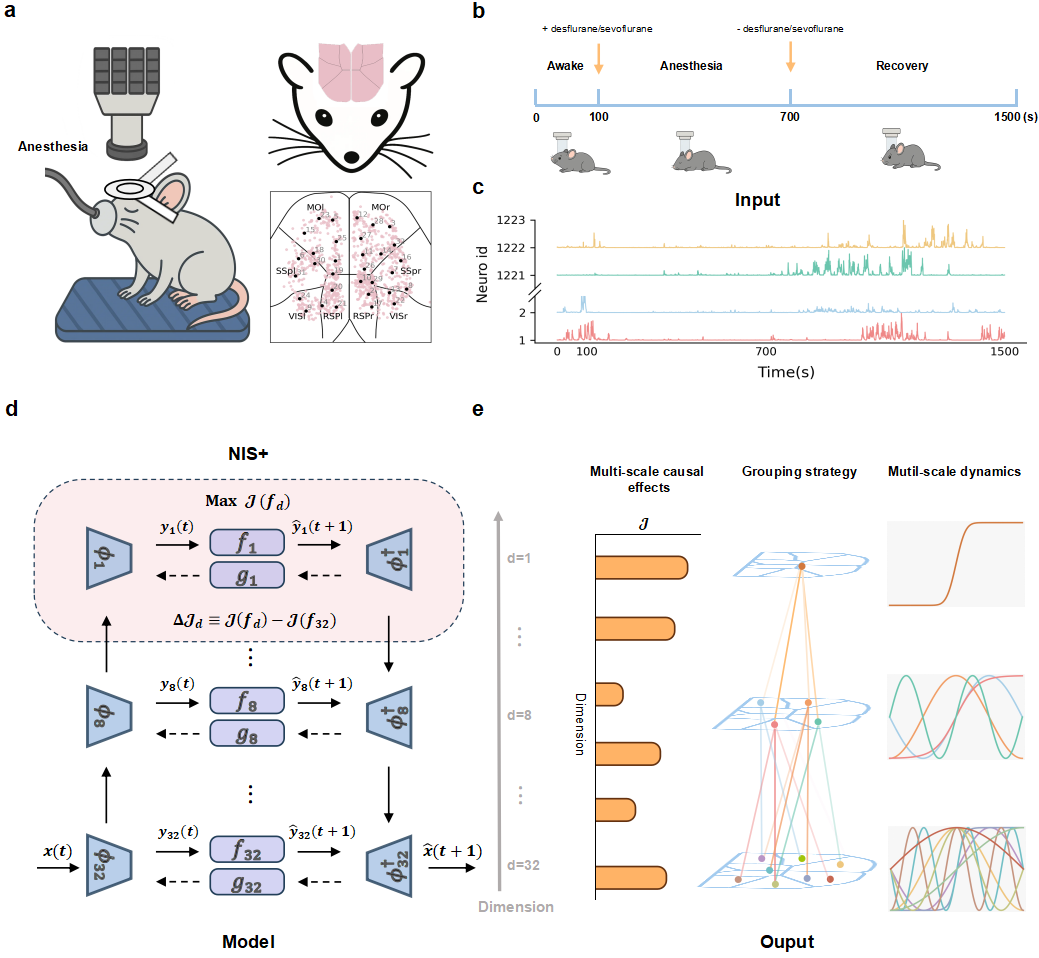
意识横跨宏观体验与微观神经活动，但连接这两个尺度仍具挑战性。现有主流理论（如整合信息理论）往往聚焦单一尺度，忽视了因果效力及其动力学如何在跨尺度上展开，以及这些过程如何依赖于信息整合。研究进展受限于跨尺度数据的匮乏，以及量化多尺度因果关系与动力学的困难。在此，我们提出一个用于多尺度动力学分析的机器学习框架，并将其应用于小鼠背侧皮层在清醒、麻醉和恢复状态下的近细胞分辨率钙信号数据。该框架通过学习层级因果变量，量化跨尺度因果效应、动力学过程及信息整合。微观层面信息的全局整合产生了潜在宏观变量，这些变量生成多尺度因果效力。当因果效力达到峰值时，一个表征意识状态的一维宏观变量随之涌现，在清醒状态下呈现亚稳态鞍点动力学特征，而在麻醉状态下则坍缩为局部化的低因果状态。这些发现建立了一个连接神经活动与意识状态的层级因果框架。

核心关注问题：

1. 意识产生在哪个尺度？宏观、介观、微观还是都存在？

2. 大脑是如何进行多层级信息聚合的？

3. 如何定量刻画大脑的意识动力学？

核心文献：

这篇文章是一种基于有效信息最大化的因果涌现识别方法，可以用于构建多尺度的大脑动力学

1. Mingzhe Yang, Zhipeng Wang, Kaiwei Liu, Yingqi Rong, Bing Yuan, and Jiang Zhang. Finding emergence in data by maximizing effective information. National Science Review, 12(1):nwae279, 2025.

这是IIT1.0整合信息论的论文，提出了意识度的衡量指标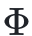, 该工作认为意识发生在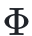值最大的子系统中。

2. Tononi, G. (2004). An information integration theory of consciousness. BMC neuroscience, 5(1), 42.

这篇文章是计算因果力分布的涌现复杂度的方法，可以用来量化大脑动力学系统中的多尺度的因果贡献分布的均匀程度

3. Erik Hoel. Causal emergence 2.0: Quantifying emergent complexity. arXiv preprint arXiv:2503.13395, 2025.

推荐阅读：

1. Luppi, A. I., Mediano, P. A., Rosas, F. E., Allanson, J., Pickard, J., Carhart-Harris, R. L., ... & Stamatakis, E. A. (2024). A synergistic workspace for human consciousness revealed by integrated information decomposition. Elife, 12, RP88173.

2. Luppi, Andrea I., et al. A synergistic core for human brain evolution and cognition. Nature Neuroscience 25.6 (2022): 771-782.

开放招募：

1. Luppi, A. I., Craig, M. M., Pappas, I., Finoia, P., Williams, G. B., Allanson, J., ... & Stamatakis, E. A. (2019). Consciousness-specific dynamic interactions of brain integration and functional diversity. Nature communications, 10(1), 4616.

2. Luppi, A. I., Cabral, J., Cofre, R., Destexhe, A., Deco, G., & Kringelbach, M. L. (2022). Dynamical models to evaluate structure–function relationships in network neuroscience. Nature Reviews Neuroscience, 23(12), 767-768.

主题五 全局神经元工作空间理论：从神经雪崩到意识广播

召集人：吴佳铭

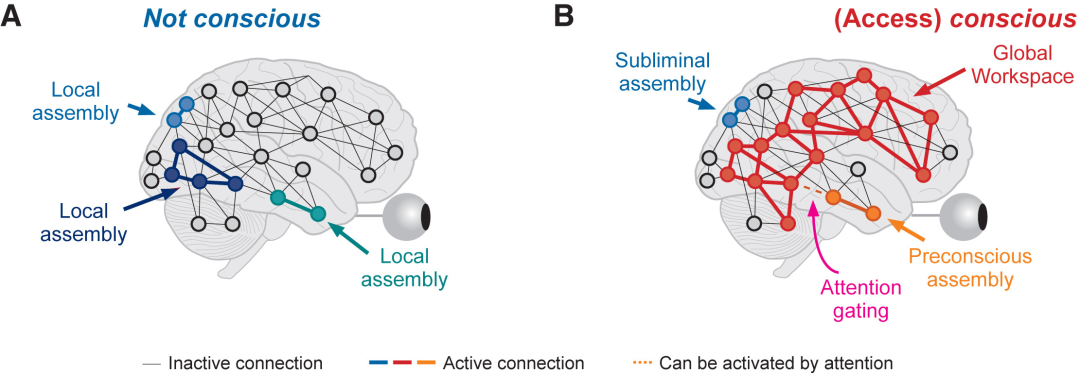
简介：全局神经元工作空间（Global Neuronal Workspace, GNW）理论是当前意识研究领域最具影响力的理论之一。GNW的核心观点认为，大脑由多个模块化的无意识处理器构成，而意识的产生过程，源于特定信息通过模块间的竞争机制进入 “全局工作空间”，并实现全脑范围的信息整合与广播。其计算模型通过微分方程模拟“神经元点火”过程，预测了神经活动的全局广播模式，将抽象理论转化为可验证的数学框架。这是一种当信息进入全局工作空间时，由局部向全脑爆发式扩散的现象，它与“神经元雪崩”等大脑临界状态下的动态模式存在深刻联系。同时，也有观点认为，在意识的 “简单问题”，如意识的神经机制和功能上，GNW取得了显著成果；但在意识的“困难问题”，即如何解释意识的主观体验上，它仍未给出答案。本期读书会，我们将从神经激活的雪崩等实验现象出发，介绍GNW的主要观点、计算模型、“全局广播” 机制与小世界网络特性等，并讨论其在“意识的难题”等方面所遇到的挑战。

核心关注问题：

1.  GNW的数学框架是什么？如何用计算模型来验证？

2. 意识来源于自下而上的“广播”还是自上而下的“整合”？

3. GNW理论能否解释主观体验这一意识“难题”？

核心文献：

最初的全局工作空间理论的核心论点，比较定性、心理学

1. Baars, Bernard J. A cognitive theory of consciousness. Cambridge University Press, 1993.

这本是比较综合性地介绍GNW的书籍

2. Dehaene, Stanislas. Consciousness and the brain: Deciphering how the brain codes our thoughts. Penguin, 2014.

这篇是Dehaene和Changeux开发的GNW的计算模型，使用微分方程模拟神经元雪崩和点火过程，预测神经活动的时空模式

3. Dehaene, S., & Changeux, J. P. (2005). Ongoing spontaneous activity controls access to consciousness: a neuronal model for inattentional blindness. PLoS biology, 3(5), e141.

一篇比较近的综述，结合实验证据进行了讨论

4. Mashour, George A., et al. "Conscious processing and the global neuronal workspace hypothesis." Neuron 105.5 (2020): 776-798.

推荐阅读：

1. Baars, Bernard J., Stan Franklin, and Thomas Zoega Ramsoy. "Global workspace dynamics: cortical “binding and propagation” enables conscious contents." Frontiers in psychology 4 (2013): 200.

2. Dehaene, Stanislas, and Jean-Pierre Changeux. "Neural mechanisms for access to consciousness." (2004): 1145-1157.

3. Shanahan, Murray. "A spiking neuron model of cortical broadcast and competition." Consciousness and Cognition 17.1 (2008): 288-303.

4. Wajnerman Paz, Abel. "The global neuronal workspace as a broadcasting network." Network Neuroscience 6.4 (2022): 1186-1204.

5. VanRullen, Rufin, and Ryota Kanai. "Deep learning and the global workspace theory." Trends in Neurosciences 44.9 (2021): 692-704.

6. Connor, Dustin, and Murray Shanahan. "A computational model of a global neuronal workspace with stochastic connections." Neural Networks 23.10 (2010): 1139-1154.

社区招募：

这是近年意识科学领域最受关注的一系列理论对抗性协作之一，本文主要是全局神经元工作空间理论和整合信息论的实验测试结果

1. Cogitate Consortium., Ferrante, O., Gorska-Klimowska, U. et al. Adversarial testing of global neuronal workspace and integrated information theories of consciousness. Nature642, 133–142 (2025).

推荐阅读：Nature意识之争：两大理论首次正面对决

非常全面地综述了各种主流意识理论

2. Seth, A.K., Bayne, T. Theories of consciousness. Nat Rev Neurosci23, 439–452 (2022).

推荐阅读：意识理论综述：众多竞争的意识理论如何相互关联？

主题六 基于人工智能的多尺度脑网络连接建模

召集人：李宗晟

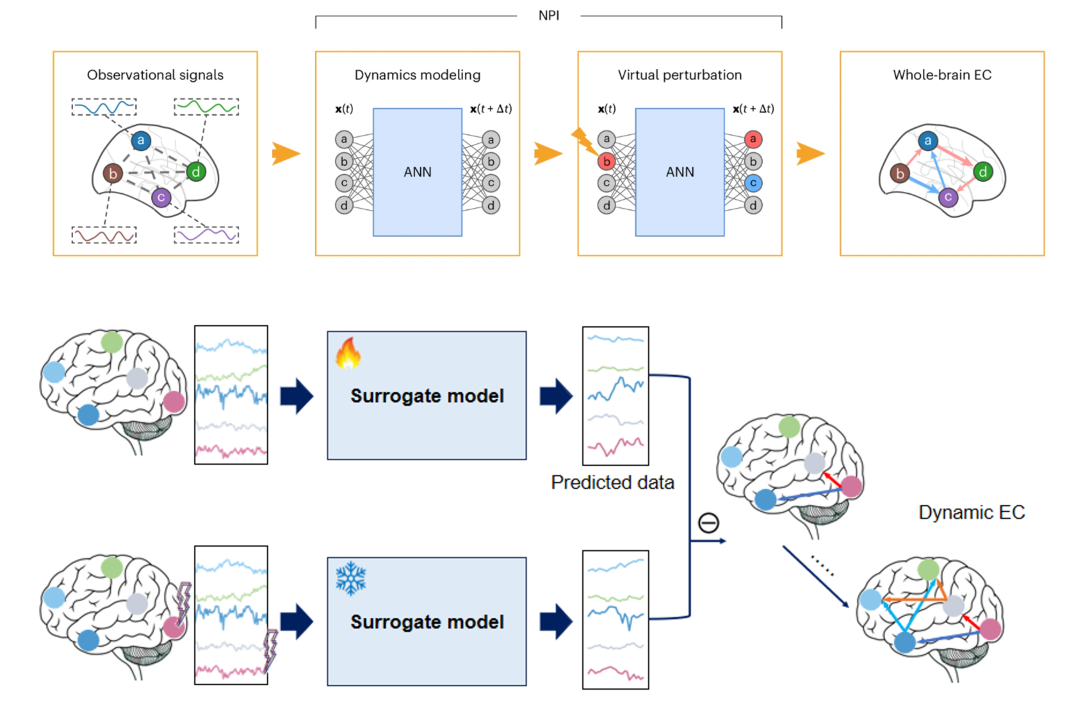
脑网络的组织具有明显的多尺度特征：在脑科学研究中，理解脑网络内如何跨越不同尺度的连接与互动，始终是重要的科学问题之一。从单个神经元的微观突触，到脑区之间的中观网络，再到全脑范围的宏观动力学，大脑呈现出多层次的网络结构与时序活动。不同层次的脑网络连接也展示了不同的意义。结构连接（SC）描述了神经元/脑区之间的解剖性连线。功能连接（FC）描述了神经信号的在时间上的协变关系。有效连接（EC）则更进一步，揭示信息流动的方向和机制。而无论是记忆与意识等高级功能，还是脑疾病的诊断与干预，往往都依赖于脑区间的有向信息流。对脑内因果关系的建模一直是很有价值的问题，但传统的建模方法往往只聚焦于某一单一尺度，难以解释跨尺度的相互作用与复杂涌现机制。近年来，人工智能的蓬勃发展为跨尺度连接建模提供了新的契机。通过结合脑科学先验知识与数据驱动的建模方法，人工智能能够自动学习不同尺度下的潜在因果关系，并量化跨尺度的动力学模式。本期读书会，我们将从不同层级的脑网络连接出发，通过多层神经网络、跨模态建模与对齐、因果推断与AI可解释性分析，讨论多尺度脑网络链接建模的意义与可行性。

核心关注问题：

1. 用怎样的模型拟合不同尺度的神经数据，如何基于稀疏数据实现稳健的跨尺度建模？

2. 不同层次的脑网络连接怎么定义，有怎样的意义，如何分析？

3. 当没有 ground truth 脑连接时，如何验证模型训练的充分性与合理性？

核心文献：

Friston 是最早明确区分了功能连接与有效连接的学者。这两篇文章分别完成了：提出了两者的差异，系统性的阐述了不同层次连接的区别。是本专题讨论的科学问题的核心背景。

1. Friston, K. J. (1994). Functional and effective connectivity in neuroimaging: A synthesis. Human Brain Mapping, 2(1–2), 56–78. Friston (2011). Functional and effective connectivity: a review. Brain Connectivity, 1(1), 13–36.

这篇文章提出了用人工智能做AI孪生脑，并用虚拟扰动构建全脑连接组的通用框架。

2. Luo, Z., Peng, K., Liang, Z. et al. Mapping effective connectivity by virtually perturbing a surrogate brain. Nat Methods22, 1376–1385 (2025).

这篇文章提供了一种可解释性更强的人工智能脑网络建模脑网络的方法。

3. Lu, Z., Zhang, W., Le, T., Wang, H., Sümbül, U., SheaBrown, E. T., & Mi, L. (2025, January). NetFormer: An interpretable model for recovering dynamical connectivity in neuronal population dynamics. In The Thirteenth International Conference on Learning Representations.

推荐阅读：

1. Kim, S. et al. Whole-brain mapping of effective connectivity by fMRI with cortex-wide patterned optogenetics. Neuron111, 1732–1747 (2023).

2. Park, H.-J., & Friston, K. Structural and functional brain networks: from connections to cognition. Science 342, 1238411 (2013).

3. Seguin, C., Sporns, O., & Zalesky, A. Brain network communication: concepts, models and applications. Nat. Rev. Neurosci. 24, 557–574 (2023).

4. Friston, K. J., Kahan, J., Biswal, B. & Razi, A. A DCM for resting state fMRI. NeuroImage 94, 396–407 (2014).

5. Lappalainen, J.K., Tschopp, F.D., Prakhya, S. et al. Connectome-constrained networks predict neural activity across the fly visual system. Nature634, 1132–1140 (2024).

6. Stepaniants, George, Bingni W. Brunton, and J. Nathan Kutz. "Inferring causal networks of dynamical systems through transient dynamics and perturbation." Physical Review E 102.4 (2020): 042309.

7. Randi, Francesco, Anuj K. Sharma, Sophie Dvali, Andrew M. Leifer, et al. “Neural Signal Propagation Atlas of Caenorhabditis elegans.” Nature, vol. 623, 2023, pp. 406–414. DOI:10.1038/s41586-023-06683-4.

开放招募：

本文简要综述了用于评估结构–功能关系的动力学建模方法，为理解脑网络中解剖约束与功能活动之间的耦合提供了理论框架，是开展多尺度连接建模的重要参考。

1. Luppi, A. I., Cabral, J., Cofre, R., Deco, G., & Kringelbach, M. L. (2022). Dynamical models to evaluate structure–function relationships in network neuroscience. Nature Reviews Neuroscience, 23(12), 767–768.

本文系统总结了多尺度脑网络的建模思路，从微观到宏观层次揭示大脑组织的层级特征，为探索跨尺度因果机制提供了理论与方法论背景。

2. Betzel, Richard F., Andrea Avena-Koenigsberger, and Olaf Sporns. "Colloquium: Multiscale modeling of brain network organization." Reviews of Modern Physics 94.3 (2022): 031002.