自然•通讯: 复杂网络上的通用神经符号回归算法

导语

发现复杂网络动力学方程是当代科学中的一个基本挑战，利用丰富的数据可以揭示各种领域中复杂现象的形成和演化背后的隐藏模式，并辅助决策。近日， 《自然 · 通讯》杂志发表论文提出了一种通用的计算工具LLC（Learning Law of Changes），能够通过结合深度学习的出色拟合能力和预训练符号回归的方程推断能力，自动、高效且准确地学习复杂系统状态变化的符号模式。该方法在物理学、生物化学、生态学和流行病学等领域的十多个代表性场景中展现出显著的有效性和效率。

关键词：复杂网络动力学（complex network dynamics）、符号回归（symbolic regression）、神经网络（neural networks）、物理先验（physical priors）、可解释模型（interpretable models）、混沌系统（chaotic systems）。

周莉丨作者

刘家臻丨审校

集智斑图速递板块，可轻松阅读海量复杂科学精选论文，一键获取原文PDF，也可能会有对应解读视频。

论文题目：Learning Interpretable Network Dynamics via Universal Neural Symbolic Regression

斑图链接：https://pattern.swarma.org/paper/4f63d7b2-aaa9-11ef-ab2f-0242ac17000f

发表期刊：Nature Communication

复杂系统无处不在，从生物网络到社会动力学，其状态变化往往由非线性微分方程主导，却常常未知，这限制了我们对现象如流行病爆发或生态崩溃的理解。随着数据获取的便利，数据驱动方法能够帮助专家从观测中提炼模式。然而，对于高维网络动力学，现有的符号回归技术面临维度灾难和计算效率低下的挑战。本研究创新性提出LLC（Learning Law of Changes），融合深度学习与预训练符号回归，仅需少量先验知识，就能高效解析复杂网络的演化规律。通过跨领域实验验证，它不仅提升了准确性，还应用于真实场景，推动科学从“黑箱”向“白箱”转型，为揭示“变化的法则”开辟新路径。

从变化的哲学到科学的追求

自古以来，人类就试图理解世界的变化。从中国古代的《易经》到西方的辩证思维，一个共同的哲学观点是：唯一不变的就是变化本身。科学家们一直致力于发现复杂现象变化的规律，以解释、预测和调控万物，例如涌现（emergence）、混沌（chaos）、同步（synchronization）和临界现象（critical phenomena）。通常，复杂系统状态的变化通常由一组非线性微分方程主导，这些方程描述了系统内部交互和动力学演化。然而，在许多领域，如全球流行病爆发（global epidemic outbreak）、极端气候异常（extreme climate anomalies）和生物种群灭绝（extinction of biological populations），这些复杂系统对应的方程往往是未知的。

幸运的是，随着数据获取日益便利，科学家基于数据驱动的方式挖掘复杂系统的变化模式。尽管已经有许多优秀的工作致力于重建低维复杂系统动力学的符号模型[1]，如双变量剪切流方程[2]、三变量元种群流行病模型[3]，以及最多九变量的系统[4]，但推断高维网络动力学的控制方程仍然是重要且具有挑战性的任务。这主要是因为网络动力学中的节点数量通常很大。如在疫情传播中，传播区域或个体的数量从几十到数十亿不等。此外，状态维度也是多维的，导致方程中的自由变量过多，拓扑交互呈指数级增长，从而增加了推断符号模型的复杂性。

目前的前沿研究主要有两种方法。第一种是两阶段稀疏符号回归（TPSINDy）[5]，它将控制函数参数化为预定义基本函数项的可学习线性组合。虽然方程推断效率高，但预定义函数项的合理性直接影响结果，需要充分准确的领域专业知识。另一种方法是使用图神经网络（graph neural networks, GNNs）来参数化控制函数[6]，克服了过度依赖专家知识的问题。然而，由于使用遗传编程（genetic programming, GP）将神经网络解析为符号方程，带来了高成本的进化搜索效率问题。

LLC：神经网络与物理先验的巧妙结合

面对这些挑战，本研究开发了一种名为LLC（Learning Law of Changes）的通用神经符号回归工具，旨在从网络动力学观测数据中自动推断常微分方程（ordinary differential equations, ODEs）。这个工具的核心是解决高维自由变量和符号推断效率低下的两大难题。

LLC的第一个关键步骤是通过神经网络和物理先验实现网络动力学信号的解耦。为了缓解高维网络动力学的维度诅咒（curse of dimensionality），研究引入了一个物理先验：网络状态的变化受自身状态和邻居状态的影响。因此，将控制方程分解为自身动力学（self dynamics）和交互动力学（interaction dynamics）两个耦合组件。网络动力学的控制方程可以被改写成按节点划分的形式：

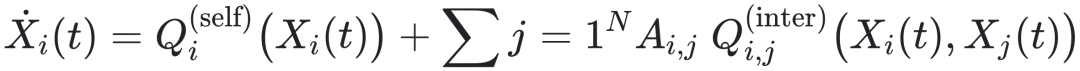
其中表示节点i状态随时间的变化率； 描述节点自身的动力学；则刻画节点i受相邻节点j影响的交互动力学；A_i,j为网络的邻接矩阵元素，指示节点i与j是否存在连接。

研究者使用多层感知机（multi-layer perceptron）参数化自身动力学的非线性，并设计了一个特殊的神经网络架构来捕捉交互动力学，包括耦合非线性项和可分解项。这种设计确保了模型能自动适应各种动力学场景。通过最小化损失函数：

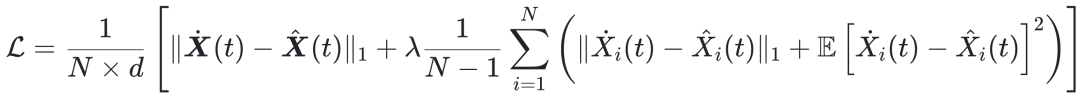
其中，N表示节点数，d表示状态维度，||·||₁ 为ℓ₁范数。损失函数的第一部分表示平均绝对误差，第二部分则表示绝对误差的方差。参数 λ 是一个用于平衡两部分的系数。该损失函数将均值和方差结合在一起，旨在不仅最小化预测值与真实值之间的平均差异，同时控制误差的波动性。

结合平均绝对误差和误差方差神经网络被训练到准确拟合状态导数，从而实现信号的稳定解耦。实验显示，这种方法比传统图神经网络 (GNNs) 更适合网络动力学学习，避免了数值积分的高计算复杂度，并提升了稳定性。

神经网络训练好后，LLC将这些“黑箱”模型解析为可解释的白箱方程。这里，研究首次引入预训练Transformer模型作为符号回归工具，以解决传统方法如遗传编程（GP）的低效率问题。预训练模型在数亿方程-数据对上训练，集成了海量方程知识，仅需单次前向传播就能从输入-输出点对中推断方程，随后可选地使用Broyden–Fletcher–Goldfarb–Shanno（BFGS）算法微调常量。这种方法大大缩短了推断时间，避免了从零开始的搜索。这里研究者选择的是NSRA模型，因为它在预训练模型中表现最佳。为了适应时间相关的网络动力学数据，他们采用K-Means采样策略，确保数据点的独立性和代表性，从而提升回归准确性。通过这个模块，LLC能高效地将拟合好的神经网络转化为符号方程，形成完整的发现管道。

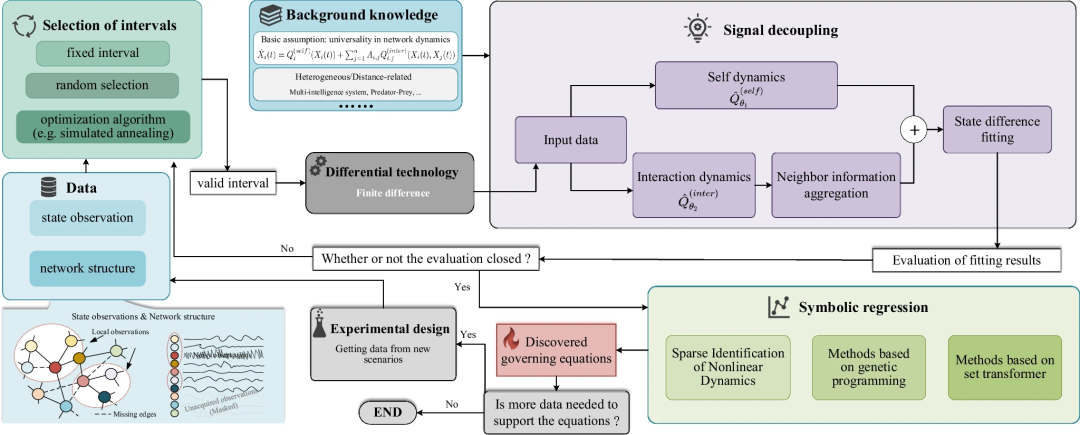
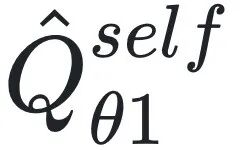图1：LLC（Learning Law of Changes）的整体流程。观测数据可以从新场景的初始实验中获取，包括系统状态随时间的变化和拓扑结构，即O＝{X_(t), A}（节点状态+网络拓扑）。然后，使用间隔选择策略选择有效间隔数据，通过有限差分在X_i(t)上获取导数，即。通过整合物理先验，神经网络和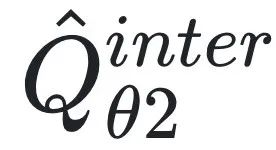，用于解耦网络动力学信号并实现变量减少，直到满足拟合要求。在获得良好拟合的神经网络后，使用符号回归技术高效解析它们的近似白箱方程。当然，如果需要额外观测数据来支持发现，可以重新审视实验设计，直到获得满意的网络动力学控制方程，从而打破循环。

LLC模型的有效性验证

一维网络动力学的推断验证

为了全面评估LLC的有效性，研究者在六个代表性的一维同质网络动力学模型上进行了测试，包括生化动力学（Biochemical dynamics）、基因调控动力学（Gene regulatory dynamics）、互惠互动动力学（Mutualistic Interaction dynamics）、Lotka-Volterra动力学、神经动力学（Neural dynamics）和流行病动力学（Epidemic dynamics）。这些模型广泛应用于生物、生态和神经科学等领域，模拟在Erdős–Rényi网络上生成连续状态数据，然后从观测中重建方程。与最先进的TPSINDy和GNN+GP方法相比，LLC在预测准确性（adjusted R²分数）和方程召回率（Recall）上显著优越。即使在噪声干扰或拓扑不完整的情况下，LLC也能维持接近零的均方误差（mean squared error, MSE），得益于神经网络的鲁棒拟合和损失函数的方差最小化。时间效率上，LLC仅需约6.5分钟完成回归，远低于GNN+GP的12.9分钟，同时无需TPSINDy那样的强先验知识库。这表明LLC在平衡效率和准确性上取得了良好成果。

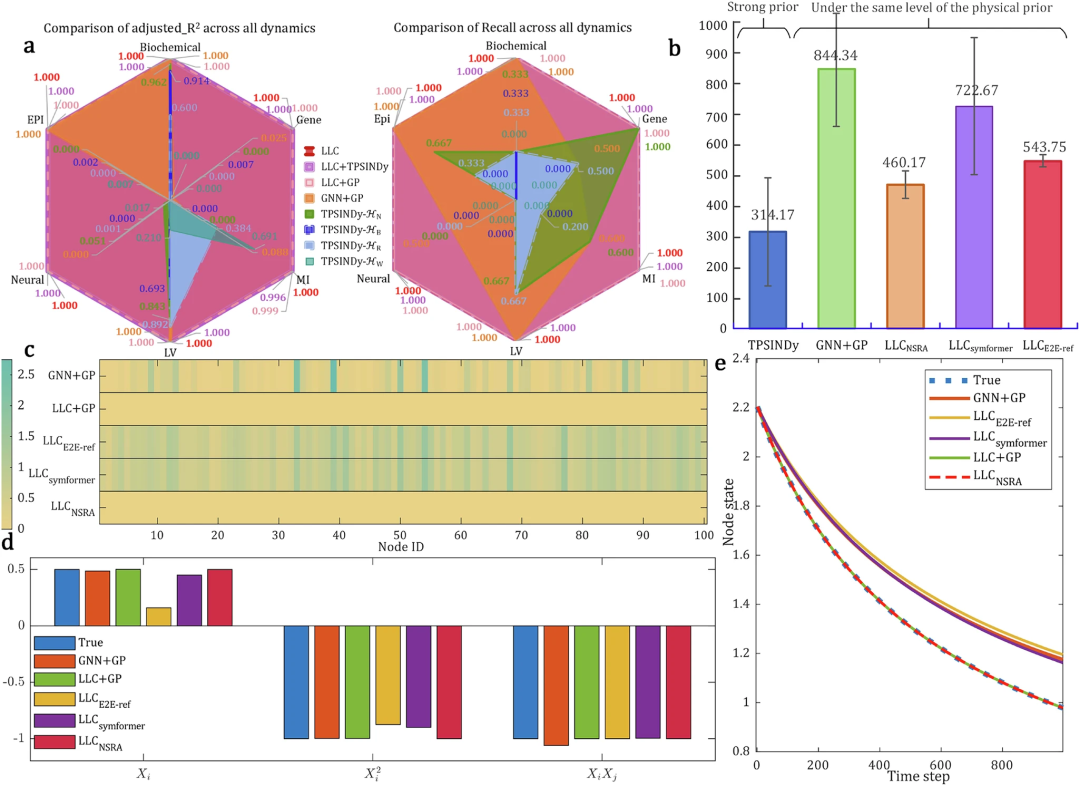
图2：推断一维同质网络动力学的结果。a. 在六个场景中，对预测准确性（adjusted R²分数）和发现方程（Recall）的比较。TPSINDy的结果高度依赖其函数项的选择，LLC在所有网络动力学场景中显著优于比较方法。b. 各种方法在所有动力学上的平均执行时间比较。请注意，TPSINDy需要强先验，即自身和交互动力学的可分解性，以及预定义的正交基本函数项。相比之下，其他方法基于相同水平的假设，即仅需可分解性。通过结合基于Transformer的预训练符号回归，LLC在效率和准确性之间实现了良好平衡。c. 在LV场景中，由发现的控制方程产生的预测结果与真实结果之间的归一化估计误差（Normalized Estimation Error, NED）。d. 各种方法发现的控制方程中拟合系数的比较。e. 单个节点的状態预测曲线的比较。

多维和异质网络动力学的挑战应对

LLC进一步扩展到多维系统，如FitzHugh–Nagumo（FHN）神经动力学和捕食者-猎物（predator-prey, PP）系统。FHN是一个二维模型，捕捉神经元放电行为，在Barabási–Albert网络上模拟脑功能区互动。通过设置掩码（masks）处理局部观测，LLC有效解耦自身和交互动力学，生成的方程比TPSINDy更接近真实形式，并在长期预测中保持周期性。同样，在异质PP系统中，节点分为捕食者和猎物角色，LLC通过多组神经网络处理不同类型交互，成功捕捉环状平衡状态，而TPSINDy虽形式匹配但预测轨迹偏差大。这突显了LLC无需强先验的优势，并在真实拓扑如C. elegans和Drosophila网络上表现出色。

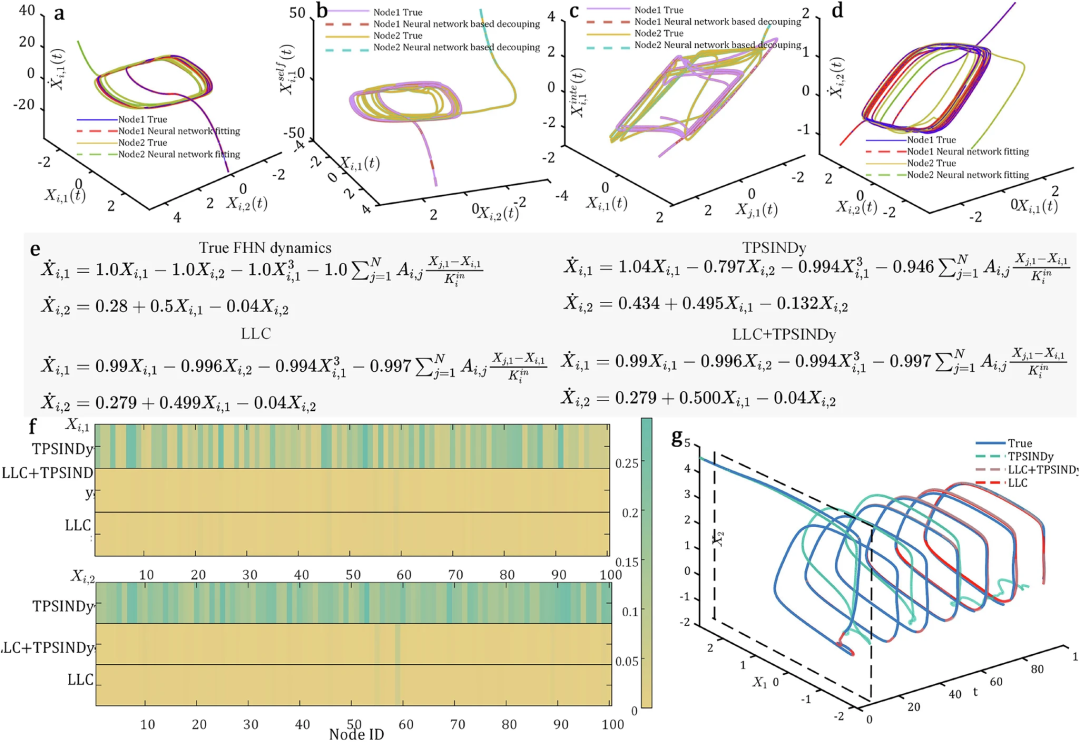
图3：推断FitzHugh–Nagumo（FHN）动力学的结果。a. 神经网络对一个节点第一维度的拟合结果。b. 一个节点第一维度自身动力学的解耦结果。c. 一个节点第一维度交互动力学的解耦结果。d. 神经网络对一个节点第二维度的拟合结果。e. 各种方法推断的控制方程的比较。f. 由推断方程生成的轨迹与真实方程生成的轨迹之间的归一化欧氏距离（Normalized Euclidean Distance, NED）的比较，横轴表示节点索引。g. 在Barabási–Albert网络上，由推断方程和真实方程生成的轨迹的比较。

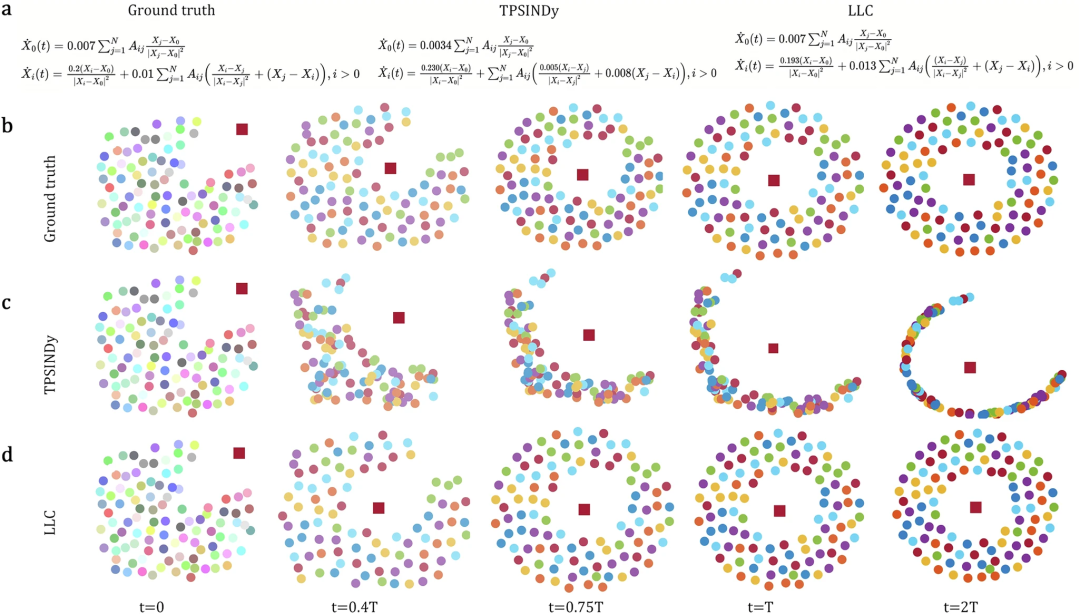
图4：推断捕食者-猎物（PP）系统的结果。a. 各种方法推断的控制方程的比较。b. 随时间变化的捕食者（方块）和猎物群（点）的真实位置。c. 由TPSINDy推断的控制方程生成的预测位置。d. 由LLC推断的控制方程生成的预测位置。

混沌系统动力学的深入剖析

研究还针对三维混沌系统如Lorenz和Rössler动力学进行了测试，考察初始条件敏感性。无论初始值固定或从分布采样，LLC推断的方程高度相似，能在1000时间步内准确预测吸引子轨迹，随后显现蝴蝶效应（butterfly effect）。在Rössler系统中，LLC恢复的分岔图（bifurcation diagram）精确再现从周期1到混沌的过渡，证明了其在分析未知动力学属性如周期倍增（period-doubling）方面的潜力。

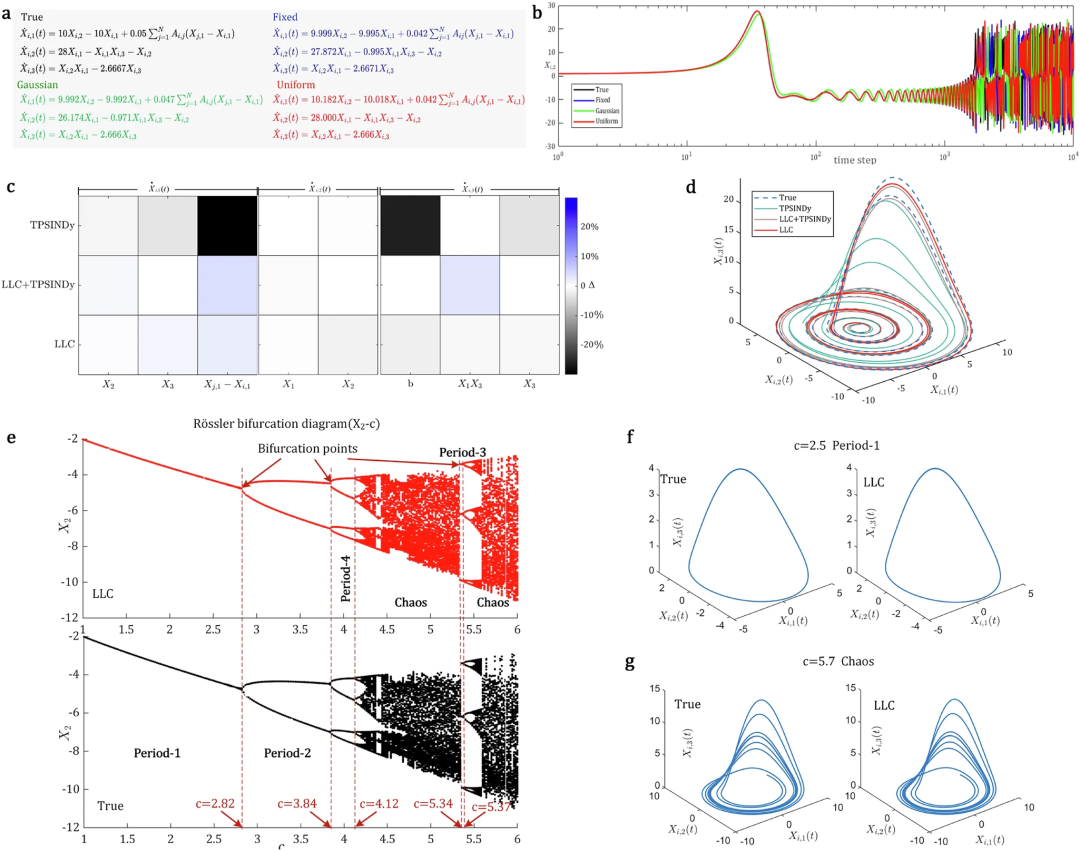
图5：推断混沌系统动力学的结果。a. 在不同初始条件下，我们的LLC推断的控制方程的比较，对耦合Lorenz系统。b. 由不同初始条件下LLC推断的方程产生的同一初始值的吸引子预测状态的比较。c. 每个方法在Rössler系统上推断的方程与真实方程之间系数误差的比较。d. 由TPSINDy、LLC和LLC+TPSINDy推断的控制方程生成的同一吸引子的状态比较。e. 通过Poincaré截面方法得到的Rössler系统的分岔图，横轴表示参数c（范围从1到6），纵轴表示吸引子第二维度状态(X_i,2) 。发现的方程展现出与真实方程相同的周期倍增和混沌现象。f. 在周期1时的极限环比较，即c=2.5。g. 在c=5.7时的混沌比较。

真实世界系统的实际应用

LLC在真实系统中表现出色，例如全球COVID-19传播数据和行人运动轨迹。在航空网络上分析早期疫情，LLC发现的方程强调自身动力学的主导作用，交互项类似于生态互惠动力学，能在不同节点度下实现准确预测，而TPSINDy易过估或低估。同样，在行人动力学中，LLC捕捉到“领地效应”（territorial effect），包括距离因素，导致人群聚集和排队现象，与真实轨迹高度一致，优于传统社会力模型（social force models, SFM）。这些应用验证了LLC在未知变化模式下的实用性。

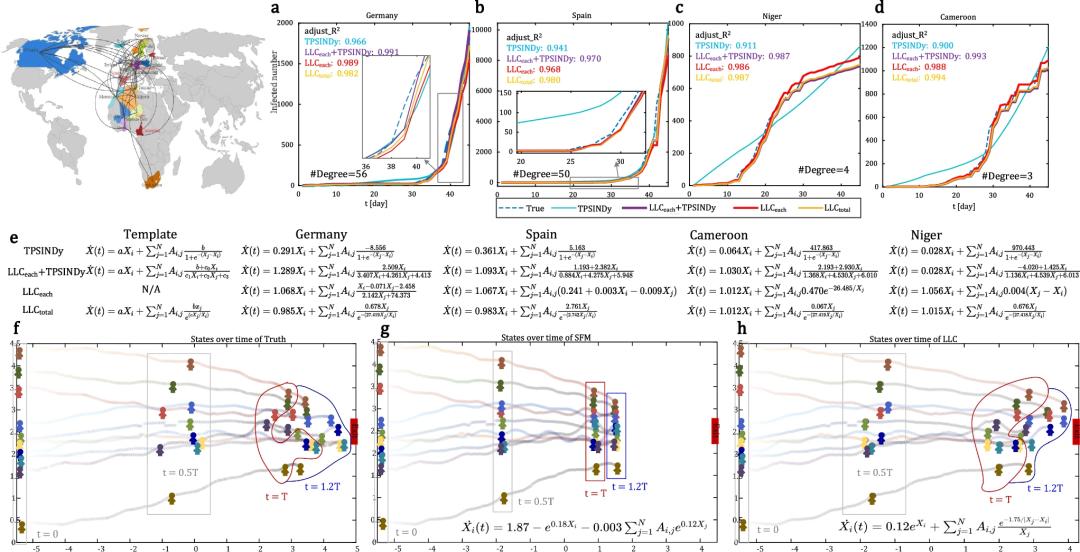
图6：推断真实系统动力学的结果，包括全球COVID-19传播和行人动力学。a–d. 各种国家或地区随时间变化的病例数比较，由TPSINDy、LLCeach+TPSINDy、LLCeach和LLCtotal生成。e. 四个代表性国家或地区的各种方法推断的控制方程的比较。请注意，LLCeach+TPSINDy中的模板是我们LLC为每个节点生成的方程的归纳。f. 随时间变化的真实行人运动轨迹，其中T之前的数据用于学习。g. 使用主流社会力模型（SFM）对行人动力学的推断结果。h. 使用我们的LLC对行人动力学的推断结果。

讨论：工具的潜力与未来展望

总之，LLC提供了一种高效准确的解决方案，通过信号解耦和预训练符号回归，揭示了从生物到混沌系统的动力学方程。它在噪声和不完整数据下的鲁棒性，以及在多维异质系统中的通用性，展示了其推动科学发现的潜力。然而，挑战仍存，如未知拓扑结构和外部扰动。未来，可扩展到非确定系统（non-deterministic systems）和高阶交互（higher-order interactions），甚至与大语言模型（large language models, LLMs）结合，助力AI代理决策。这项工作如一个“数字培养皿”，为应对新疫情或气候变化铺平道路。

参考文献

1. Makke, N. & Chawla, S. Interpretable scientific discovery with symbolic regression: a review. Artif. Intell. Rev. 57, 2 (2024).

2. La Cava, W. et al. Contemporary symbolic regression methods and their relative performance. Adv. Neural Inf. Process. Syst. 2021,1 (2021).

3. Lipshtat, A., Alimi, R. & Ben-Horin, Y. Commuting in metapopulation epidemic modeling. Sci. Rep. 11, 15198 (2021).

4. Udrescu, S.-M. & Tegmark, M. AI Feynman: a physics-inspired method for symbolic regression. Sci. Adv. 6, 2631 (2020).

5. Gao, T. T. & Yan, G. Autonomous inference of complex network dynamics from incomplete and noisy data. Nat. Comput. Sci. 2,160–168 (2022).

6. Zang, C. & Wang, F. Neural dynamics on complex networks. In Proc.26th ACM SIGKDD International Conference

详情请见：复杂网络上的自组织与集体行为：从扩散、相变到博弈 | 读书会启动

6. 高考分数只是张入场券，你的科研冒险在这里启航！

7. 系统科学前沿十讲：理解自然、生命与社会的复杂性