图神经网络(GNN)作为几何深度学习中的关键模型,在分子性质预测方面已经取得了显著成功。与此同时,Kolmogorov-Arnold网络作为多层感知机的有力替代方案,展现出更强的表达能力、更高的参数效率以及更好的可解释性。
为了结合这两种框架的优势,山东大学王光辉以及南洋理工大学夏克林团队于2025年8月11日在《Nature Machine Intelligence》共同发表文章,题为“Kolmogorov-Arnold graph neural networks for molecular property prediction”。

文章提出了Kolmogorov-Arnold图神经网络(KA-GNN),将KAN模块融入GNN的三个基本组成部分:节点嵌入、消息传递和读出。在KAN中引入基于傅里叶级数的单变量函数,以增强函数逼近能力,并提供理论分析来支持其表达力。进一步设计了两种架构变体:KA-GCN和KA-GAT,并在七个分子基准数据集上进行了评估。实验结果表明,KA-GNN在预测精度和计算效率方面均显著优于传统GNN。更重要的是,模型在可解释性上也有所提升,能够突出化学上具有意义的子结构。这些发现表明,KA-GNN为分子数据建模、药物发现及更广泛的应用提供了一个强大且可推广的框架。
KA-GNN仓库链接:
https://github.com/LongLee220/KA-GNN
背景
基于分子的人工智能模型可分为两大类:分子特征驱动的机器学习与端到端深度学习。第一类方法依赖分子描述符或分子指纹作为机器学习模型的输入特征。其核心过程是分子特征化,即基于分子的结构、物理、化学或生物学属性提取或生成特征。其中,基于结构的描述符或指纹,尤其是源自拓扑方法的特征,已被证明具有极高的有效性。将这些基于拓扑的分子特征与机器学习模型相结合,在药物设计的多个阶段均取得了显著成果,例如蛋白-配体结合亲和力预测、蛋白突变分析等。第二类方法包括端到端的深度学习模型,这类模型直接使用不同的分子表示并结合多种深度学习架构。尤其是几何深度学习(GDL)模型,如图卷积网络(GCN)、图自编码器、图Transformer等,已被广泛应用于分子数据分析和药物设计。然而,传统基于共价键的分子图表示存在一定局限,而引入非共价相互作用已被证明能显著提升模型性能。这表明,新型图表示方式有望优于传统的共价键分子图。通过将几何和拓扑驱动的分子图融入GDL模型,可以提升模型性能,并深入揭示分子结构与功能。
Kolmogorov-Arnold网络(KAN)基于Kolmogorov-Arnold表示定理,正逐渐成为传统多层感知机(MLP)的有力替代。与采用固定权重和节点激活函数的传统MLP不同,KAN在边上引入可学习的单变量函数,从而实现对复杂函数的高精度、可解释建模。更为重要的是,KAN模块已被嵌入GNN,以替代其在节点嵌入、消息传递与读出中的MLP。在此,作者提出一个统一框架KA-GNN,将KAN全面融入GNN的三大核心组成部分:节点嵌入、消息传递和读出。设计了基于傅里叶的单变量函数,有效捕捉图中低频与高频的结构模式,从而增强特征嵌入与消息聚合的表达能力。在七个基准数据集上的大量实验验证了KA-GNN在预测精度与计算效率上的优势,确立了其作为处理非欧几里得数据的一种几何深度学习新范式的潜力。
方法
KAN的灵感来源于Kolmogorov-Arnold叠加定理,该定理表明任意多元连续函数都可以表示为有限个单变量连续函数与二元加法运算的组合。相应地,KAN通过将每一层构建为若干可学习一元函数的和来实现这一思想,与叠加形式一致。每个函数都作为可学习的预激活函数,提供了比固定非线性函数(例如ReLU)更灵活的替代方案。这使得KAN能够使用更少的参数并展现更平滑的梯度,从而实现更紧凑且更精确的函数逼近。在本研究中,作者通过引入傅里叶级数作为KAN预激活函数的基函数扩展了KAN。与此前基于B样条函数的实现相比,基于傅里叶的模型能够有效捕捉图结构中的低频与高频模式。全局三角函数的使用带来了平滑而紧凑的表示形式,有助于梯度传播与参数高效性。
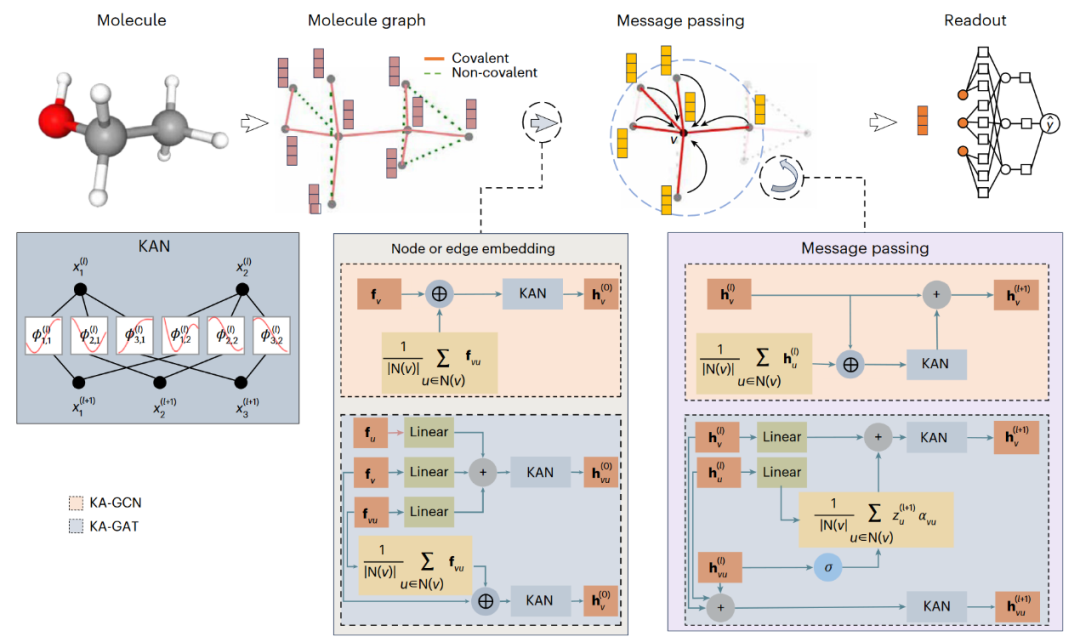
图1 KA-GNN模型架构
KA-GCN在标准GCN的基础上引入KAN层,替代传统基于MLP的变换。在KA-GCN中,每个节点的初始嵌入通过以下方式计算:将其原子特征(如原子序数、原子半径)与邻居化学键特征(如键类型、键长)的平均值拼接后输入至KAN层。该设计通过数据驱动的三角函数变换同时编码了原子身份与局部化学环境。消息传递层遵循GCN机制,而节点特征则通过残差KAN进行更新,替代传统的MLP。KA-GAT同时考虑边的嵌入,节点与边特征均通过KAN层进行初始化。每条边的嵌入由其化学键特征与两端原子的特征融合而成,从而形成具备上下文感知的键表示。在消息传递过程中,注意力权重由边嵌入计算得到,随后节点与边特征均通过KAN层迭代更新。这一机制支持自适应注意力与丰富的特征交互,覆盖共价键与非共价键。通过用KAN驱动的映射替代静态聚合与固定的MLP,KA-GCN与KA-GAT能够实现更灵活、更具表达能力的分子图建模。
在将KA-GCN与KA-GAT应用于分子数据时,将每个分子表示为一个图,其中原子作为节点,共价与非共价相互作用作为边。具体而言,当两个原子存在化学键或其空间距离小于5Å时,在它们之间建立一条边,从而同时捕捉局部化学键与长程依赖关系。
结果
基本性能
为了评估KA-GNN的性能,选取了MoleculeNet中七个广泛使用的基准数据集。其中,MUV、HIV和BACE属于生物物理学领域,BBBP、Tox21、SIDER和ClinTox属于生理学领域。在七个数据集上的对比分析中,评估了多种GDL模型,还纳入了其他基于KAN的GNN架构,如 GNN-SKAN、GraphKAN和KA-GNNs。
表1 KA-GNN与最新GDL模型在不同分子性质预测数据集上的性能比较
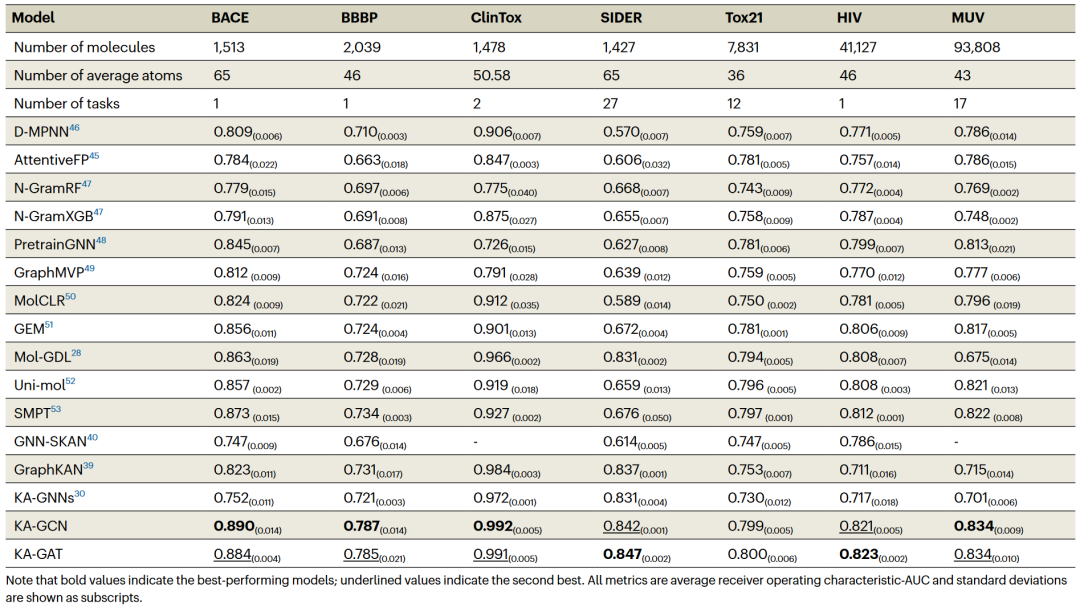
表1的对比结果进一步验证了KA-GNN模型的优越性,在所有基准数据集上均取得了当前最优性能,尤其在ClinTox和MUV等复杂且具有挑战性的数据集上表现突出。这表明KA-GNN在分子数据处理上的强大能力。
表2 KA-GNN在三种基函数(B样条、多项式与傅里叶级数)下的性能比较
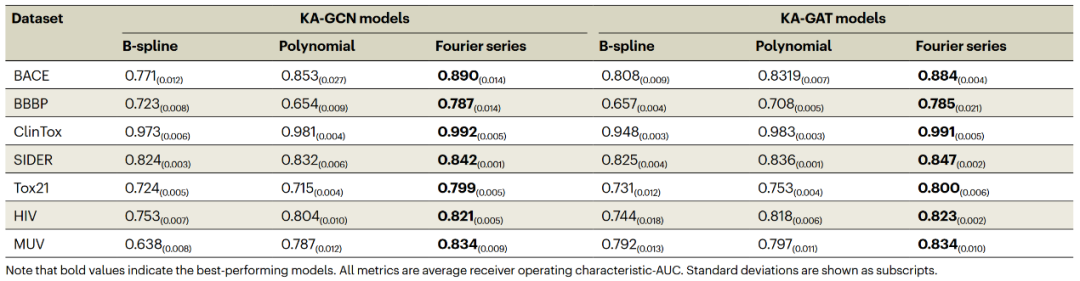
表2显示了KA-GNN在各数据集上的持续性能提升,进一步验证了其在分子任务中的有效性。基于傅里叶的KAN具有更强的表达能力。此外,消融实验揭示傅里叶KAN不仅提升了预测精度,还改进了特征嵌入、消息传递和最终预测等关键阶段。
表3 GCN/GAT与其基于傅里叶级数的KA-GCN/KA-GAT性能比较
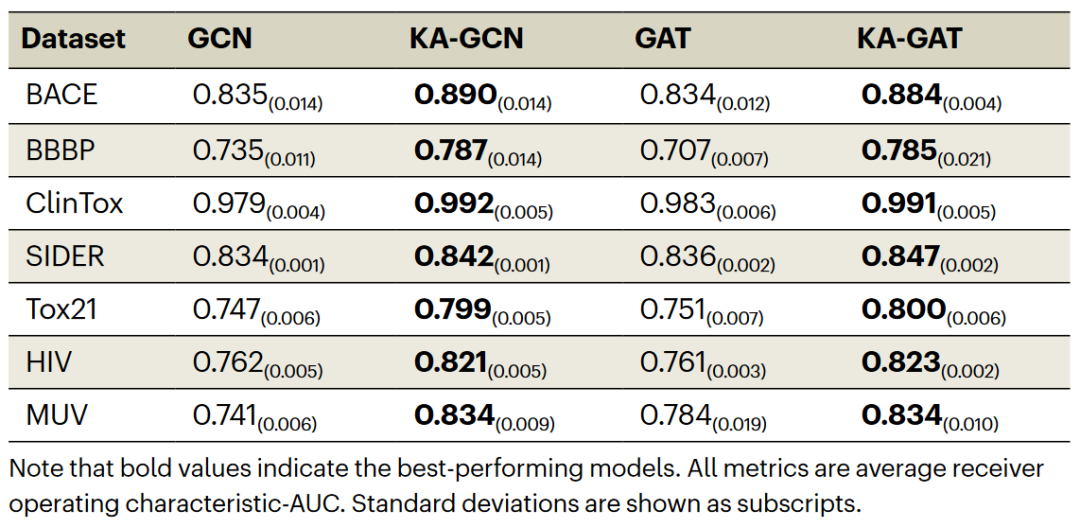
作者还在相同的分子图输入下,将标准GCN/GAT与其对应的KA-GNN版本(使用傅里叶级数)进行了比较。如表3所示,KA-GNN在所有任务中均显著优于基线模型,凸显了傅里叶KAN在捕捉化学结构表示方面的增强能力。
基于傅里叶的KAN在GNN中的效率
如图2a、2b所示,基于傅里叶的KAN模型(a.KA-GCN. b.KA-GAT)在运行时间上始终优于B样条KAN以及基于MLP的GCN/GAT。这种效率得益于正弦基函数的全局特性,使得模型能够以更少的可训练参数实现紧凑的函数逼近。
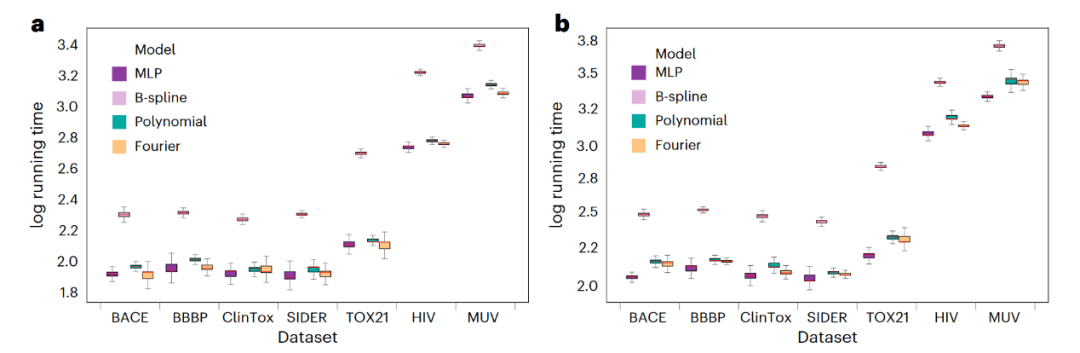
图2 MLP模型与不同基函数下KA-GNN的效率对比
与采用大型稠密权重矩阵的MLP不同,KAN使用固定的基函数及轻量级的可学习系数,从而显著降低了计算成本。虽然B样条KAN的参数量也较少,但其局部控制点和插值步骤会引入额外开销。相比之下,傅里叶基函数提供了平滑的全局逼近,避免了这些负担。基于傅里叶的KA-GNN在效率上同样优于传统的GCN和GAT。GCN的计算复杂度随节点数和层数增加而上升,GAT的开销则与注意力头数相关;而傅里叶-KAN通过消除冗余的参数矩阵简化了消息传递过程。这不仅加快了模型收敛,也缩短了训练时间,尤其适用于大规模图学习任务。
KA-GAT分析的可解释性
为验证KAN模块的可解释性,对KA-GAT在分子 Fc1ccc(NC(=O)c2ncc(cc2)C#N)cc1[C@]1(N=C(OCC1)N)C上的预测进行了分析。图3a、3b展示了其二维与三维结构,作为化学参考。图3c给出了显著性图,突出显示了原子与键对预测的重要性(颜色越亮,重要性越高)。图3d则展示了基于掩码的GNNExplainer生成的子图重要性分析,突出影响预测的关键官能团。综上,KA-GAT能够识别化学上相关的特征(如氟基与酰胺基团),从而提供具有可解释性且符合领域知识的预测结果,支持其在药物发现中的应用价值。
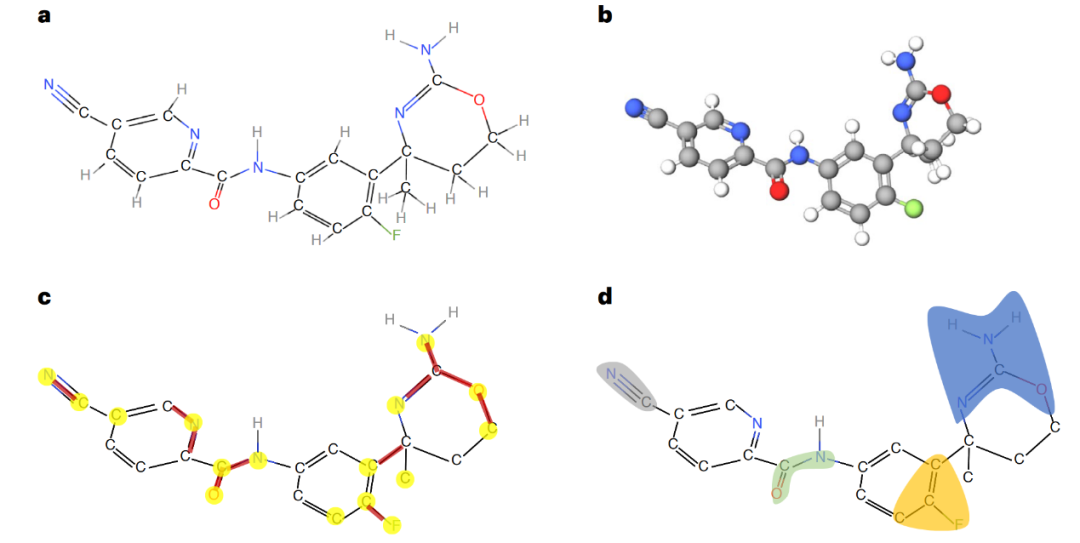
图3 KA-GAT对测试分子的可解释性
讨论
KA-GNN将KAN模块有机地融入GNN架构中,并具有三项核心创新。首先,在分子图构建方面,不仅考虑了共价相互作用,还通过基于截断距离引入边来纳入非共价相互作用。这一方法使KA-GNN能够捕捉更广泛的分子相互作用,超越传统的共价键表征,从而对分子结构及其性质形成更全面的理解。其次,将KAN融合到GNN框架中,在显著减少参数数量的同时提升了解释性与表达能力。不同于传统基于MLP的消息传递机制,KAN提供了更灵活的函数逼近方式,以更少的可训练参数实现更高的预测精度。第三,在KAN中引入基于傅里叶的激活函数,替代原有的B样条函数。傅里叶级数广泛应用于信号处理与函数逼近,使KA-GNN能够更好地捕捉图结构数据中的高频模式。通过学习与优化傅里叶系数,KA-GNN在建模复杂分子相互作用与生化系统时展现出更高的精度与稳定性。
尽管取得了令人鼓舞的性能表现,KA-GNN仍有改进空间。特别是,如何将学习到的基于傅里叶的表示与明确的化学与生物学原理相对齐,仍然是一个重要挑战。尽管显著性图与子图重要性分析表明KA-GNN能有效识别关键的分子子结构、关键原子相互作用以及功能相关子图,但尚缺乏一种能够将单个或频率相关的傅里叶函数与具体物理或化学意义相联系的深入特征重要性分析。事实上,作者尝试使用基于KAN的剪枝方法对所学习的傅里叶函数进行特征重要性分析时,并未得到具有实际意义的结果。未来一个令人兴奋的研究方向,是在模型中引入领域特定的约束,结合对比学习策略,或采用物理化学启发的傅里叶函数,从而提升KA-GNN学习表示的可解释性,并加强其与专家领域知识的一致性。
合理设计的傅里叶成分有望在有效表征与表示分子的深层物理与化学性质方面展现巨大潜力。从物理化学的角度来看,量子力学模型(如薛定谔方程、密度泛函理论、分子轨道理论等)均涉及具有调和或波动特性的性质,这些性质在数学上可表示为傅里叶型函数。从机器学习的角度来看,球谐函数已被广泛应用于几何深度学习模型,用于表征分子的等变性,而这些球谐基函数本质上正是傅里叶型函数。最后,傅里叶成分不仅可用于频率扰动分析,还能用于表征多种量子描述符,例如HOMO-LUMO能隙、原子部分电荷或对称性自适应基函数。这些研究有助于弥合图表示与分子功能及性质之间的鸿沟。
参考链接:
https://doi.org/10.1038/s42256-025-01087-7
--------- End ---------
内容中包含的图片若涉及版权问题,请及时与我们联系删除



评论
沙发等你来抢