贝叶斯X非线性——基于动态因果的复杂系统自动建模方法

导语

在神经科学领域，理解大脑各区域间因果关系对于揭示脑功能机制至关重要。然而，大脑网络的动态活动非常复杂，我们需要既考虑因果性又包含非线性的模型才能深入刻画脑区互作。动态因果建模（Dynamic Causal Modelling, DCM）正是用来解决这一问题的重要方法——它利用大脑生理动力学模型和贝叶斯推断，从脑成像数据（如EEG/MEG或fMRI）中估计不同脑区之间的有效连接关系[1][2][3]。近日，发表在《皇家学会界面期刊》的一项最新研究将概率编程语言引入DCM方法学，显著提升了模型推断的效率和准确性。研究团队开发了一套自动化的因果模型推断方案，成功应对了以往方法面临的多解不确定性等挑战，让借助脑成像数据探究神经因果机制变得更加可靠和高效。

关键词：动态因果建模，概率编程语言，神经因果机制，非线性动力系统

Zequan Liu. | 作者

周莉 | 审校

论文题目：Dynamic Causal Modeling in Probabilistic Programming Languages
论文地址：https://royalsocietypublishing.org/doi/full/10.1098/rsif.2024.0880

动态因果模型推断的挑战

要从脑电、脑磁等数据中推断隐藏的脑网络因果连接，并非易事。DCM建立在生物物理动力学方程之上，例如用微分方程描述脑区活动，然后通过模型反演来估计方程中的参数（如脑区间连接强度等）的后验概率分布。这一过程计算量巨大，因为模型通常是非线性且维度较高，直接求解精确的后验分布常常不可行。

DCM的贝叶斯推断核心公式如下：

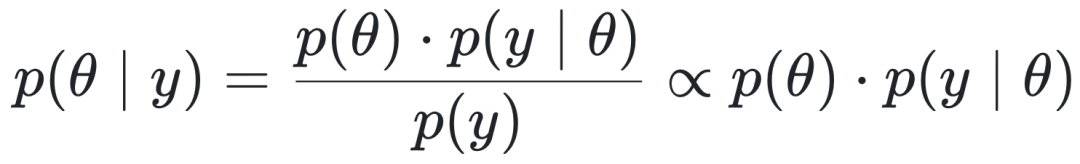
其中 θ是模型参数， y是观测数据，p(θ)为先验， p(y|θ)为似然。

传统上，许多研究采用变分推断 (Variational Inference, VI) 来近似后验分布，以将求解高维积分的问题转化为优化问题，从而大幅降低计算成本。例如DCM早期实现中使用固定形式的近似分布（如变分贝叶斯方法）来逼近参数后验。但是，这种参数化近似方法也有明显缺陷：当真实后验是多模态分布（存在多个峰）时，变分近似往往难以同时捕获多个解，并且可能低估模型不确定性。换言之，如果有多组不同参数都能解释数据，简单的近似方法可能只找到其中一个解，忽略了其它可能性，也无法给出可靠的置信区间。

过去十多年，不少学者尝试用马尔可夫链蒙特卡洛（Markov chain Monte Carl, MCMC）采样来替代变分推断，希望更完整地探索后验分布。早期工作测试了随机游走、切片采样、自适应MCMC等多种无梯度采样算法，但发现它们难以高效探索复杂模型的参数空间。虽然这些方法能在合理精度下拟合数据，但要获得充分独立的样本以准确推断生物学参数仍非常困难。随后，研究者将目光转向利用梯度信息的MCMC算法，例如Langevin动力学采样和哈密顿蒙特卡洛 (Hamiltonian Monte Carlo, HMC) [4]，希望借助模型联合概率的梯度来加速收敛。其中，HMC通过将参数空间的采样引入“动量”，利用物理哈密顿动力学辅助随机游走，从而在理论上能够更高效地探索高维后验分布。然而，在DCM这样复杂的非线性动态模型上，即便是HMC也面临挑战：一方面，每次采样迭代需要数值解ODE并计算梯度，计算开销巨大；另一方面，HMC算法本身有一些需要人工设置的超参数（如步长和模拟步数），如果设置不当，采样要么无法充分探索空间，要么数值不稳定导致采样发散。

哈密顿动力学核心方程如下：

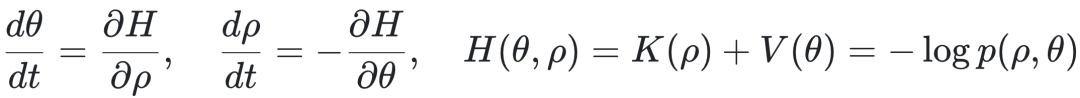
其中K(ρ)表示动能（通常假设为高斯形式），V(θ)为势能，对应目标分布的负对数。

为了在有限计算步数内近似连续轨迹，HMC 使用 Leapfrog 积分法进行数值模拟，其更新规则如下：

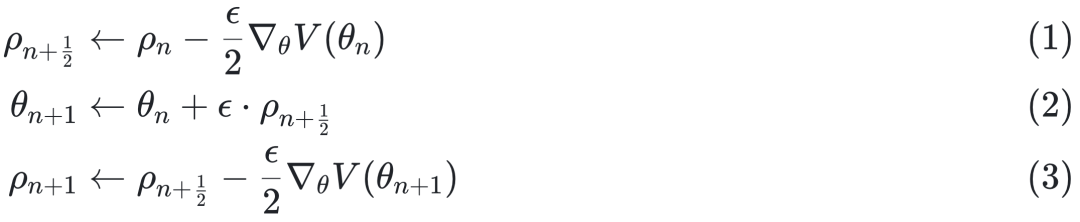
为减轻HMC参数调校的难题，研究者引入了其自适应变体——无U转采样器 (No-U-turn Sampler, NUTS) [6]，它能依据目标分布几何形状自动调整步长和路径长度。NUTS一定程度上缓解了调参问题，但在处理非线性微分方程、参数高度相关、以及观测不完备的情形时，即使有NUTS也难免出现收敛缓慢甚至无法收敛的问题。先前针对DCM的研究表明，在合理的计算时间内，要兼顾采样数目和参数估计精度极具挑战：HMC类方法产生的有效样本数偏低，导致不可靠的参数不确定性估计。更严重的是，由于大脑系统存在参数简并现象（即多组参数产生类似输出，导致模型非辨识），不同采样运行可能收敛到参数空间的不同区域（局部极值）而各自都能解释数据，从而出现多模态的后验分布。对推断算法而言，这意味着重复实验会给出截然不同的参数解集，让人难以判断哪一个才是对的，浪费大量计算资源。总而言之，DCM的推断精度和效率一直受到这些技术瓶颈的制约。

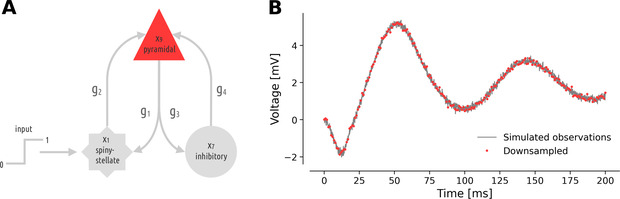
图1 动态因果模型(DCM)示意例。（A）展示了用于产生事件相关电位(ERP)的简化神经质点模型，包括三个互相连接的神经元种群：兴奋性锥体神经元（Pyramidal cells）、抑制性中间神经元（Inhibitory Interneuron）和接收外部输入的有棘星状细胞（Spiny stellate）。这些神经群体通过若干连接参数耦合在一起，外部刺激作为输入驱动系统（见黑色箭头所示因果关系）。(B) 模型仿真生成的锥体神经元电压信号（灰色曲线）及加入观测噪声并下采样后的观测数据（红点）。研究人员以此虚拟模型作为测试案例，用来评估不同推断方法对已知参数的恢复能力和对观测数据的拟合准确度。

新方法：概率编程结合DCM贝叶斯推断

面对上述困难，新研究尝试了一条不同路径：利用概率编程语言 (PPL) 的强大能力来实现DCM模型的自动化推断。概率编程语言是一类特殊的编程工具，它将传统编程结构与概率模型描述相结合，使研究者可以用高层代码方便地定义复杂的统计模型，并调用内置的先进推断算法。借助PPL，我们无需手推复杂的数学推导，只需用近似Python或Stan等语言编写模型，底层就能自动完成梯度计算、采样推断等繁琐工作。常见的PPL如Stan[7]、PyMC和NumPyro等，都内置了如变分推断和HMC-NUTS采样等高效算法，并针对复杂模型和大型数据进行了性能优化（利用自动微分和硬件加速等技术），具有灵活、高性能、可扩展的优点。

在这项研究中，作者将DCM的神经动力学模型分别用多个主流概率编程平台实现，并对比了不同框架下推断的效率和精度。一个突出亮点是，他们充分利用了JAX库提供的自动微分和GPU加速功能[9]，使得采用HMC-NUTS算法进行采样时，每单位时间获得的独立有效样本数相比以往显著提高。换言之，借助现代机器学习领域的发展，HMC这类梯度采样方法的“高昂代价”正在被大幅削减。研究结果表明，在JAX支持的NumPyro[8]等框架中，同样复杂度的模型可以更快收敛并取得比以往更多的后验样本，这为将高精度采样应用于DCM奠定了基础。

然而，仅有更快的采样并不足以解决多模态收敛问题。为此，研究团队提出了三项关键策略来增强推断可靠性：

优化采样超参数：针对NUTS采样器，细致调整其算法参数（例如目标接受率、最大树深等），相当于为采样过程“调教马力”。合理的超参数设置可避免轨迹过短导致的低效探索，也避免轨迹过长导致的重复采样和计算浪费，从而在有限计算量下更充分地探索后验分布。
广泛的初始值设定：将多个平行马尔可夫链的起始点随机置于参数先验分布的尾部（极端位置）。这种做法增加了链与链之间的多样性，防止所有采样都从同一个近似解附近出发。一些链或许会探索到此前被忽略的模式，从而提高找到全局最优解的概率。研究中发现，将初始值选在先验尾部可有效缓解以往部分链陷入局部极值的情况，使更多链收敛到正确的后验模式。
基于预测性能的加权堆叠：针对获得的多个马尔可夫链结果，不再简单地将它们混合（那可能掺入不佳的次优解），而是采用一种称为“后验堆叠”的方法。具体而言，计算每条链生成的模型对观测数据的预测准确性，根据这一预测指标给予链结果不同权重，再将它们加权融合。这样可以突出可信度高的解、淡化不可靠的次模态，从而获得更精确稳健的综合后验分布。

通过以上改进措施，该研究在一个9维状态、10个参数的典型DCM模型上成功实现了可靠的参数推断。在实验中，研究者首先用较宽松的先验对模型进行推断，观察到不同链确实会由于参数简并而收敛到不同模式，这重现了多模态问题。

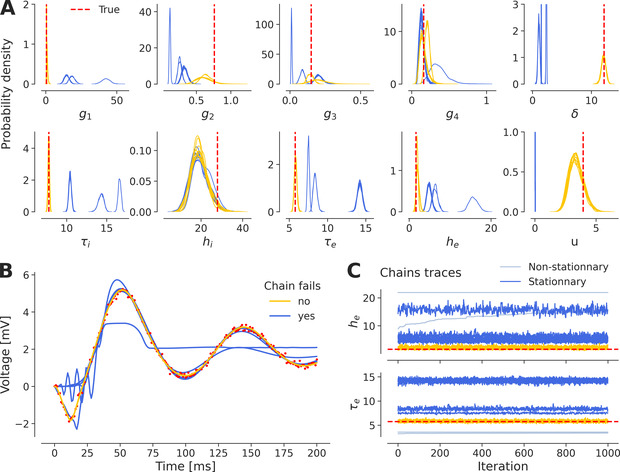
图2 推理过程中多模态出现。同一个推断过程会跑出多组截然不同的参数。多模态=收敛到不同峰；只有落在正确模态的链才重现真实动力学。蓝色链→局部极值、拟合差；黄色链→全局模态、拟合好；浅蓝链→非稳态直接踢掉。A) 24 条 NUTS 链在后验空间的分布；B) 拟合好的 vs 落到局部最优的链在时间域的动态；C) 链的稳态检查。

随后引入优化策略：调整NUTS参数并增加链初始多样性后，采样结果显著改善，80条并行链全部成功收敛并准确重现了合成数据。再通过后验堆叠整合链结果，有效滤除了伪解模式对预测的负面影响，提升了模型对数据的拟合预测性能。

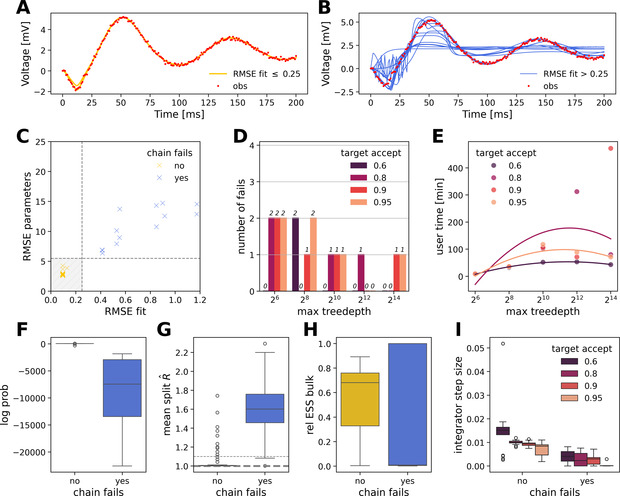
图3 超参数网格搜索。调 NUTS 的“步长/树深/接受率”的重要性。目标接受率 0.6 + 树深 2⁸ ⇒ 全部链收敛；太高接受率→步长过小，探索不够。精细调参可以求收敛，但代价高、不通用。

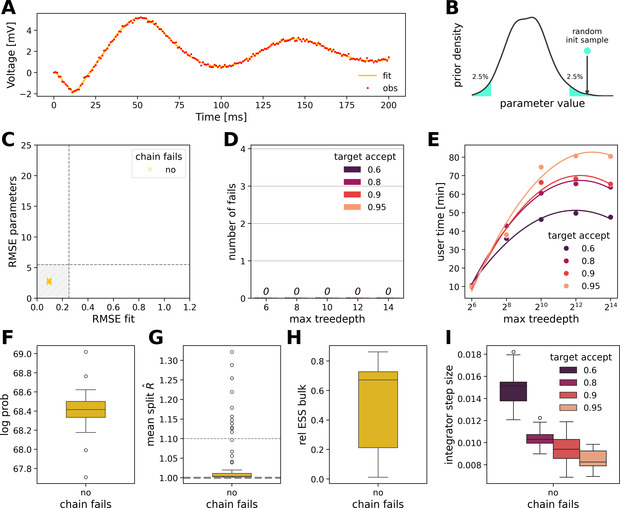
图4 尾部初始化。不用调参也让 NUTS 全部收敛。

A) 80 条“尾部初始化”链全部拟合成功；B) 初始化示意；C–D) RMSE 和失败链=0；E–I) 同 Fig 3 的诊断指标。把初始点丢到先验 2.5% 尾区 ⇒ 100% 收敛，且探索更大胆（步长大）。先验尾部起步是一键稳收敛的简洁技巧。

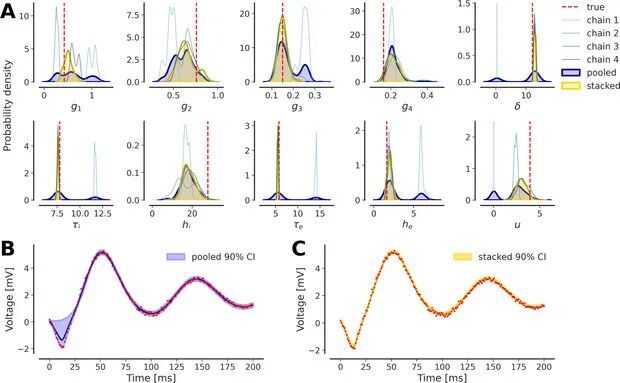
图5 后验堆叠。链分成不同模态后，如何自动剔除次优解？

A) 多模态链示意；B) 均权 pooling 仍含伪峰；C) 基于预测精度加权 stacking 消除伪峰。Stacking→黄色曲线平滑且更贴真值；Pool→蓝色仍有幻影模态。将链按预测好坏加权堆叠，可自动滤噪留精。

值得一提的是，研究还比较了变分推断与MCMC在该模型上的表现。结果显示，当采用充分灵活的变分近似（如全阶协方差的变分方法或自动拉普拉斯近似）时，其推断的后验与NUTS采样高度一致，都能够捕捉到真实参数并呈现相似的不确定性结构。

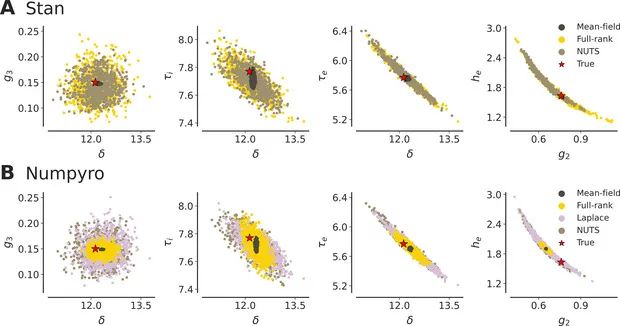
图6 VI 与 NUTS 后验对比。选取的若干关键参数，两两绘制散点密度。NUTS（浅棕）、自动 Laplace （紫灰）、Full‑rank ADVI（黄）、Mean‑field ADVI（深棕）。红点：真实生成参数位置。NUTS后验形状椭圆/弯曲，跟随相关结构，黄金标准，几何捕获最完整，但计算较慢。

反之，若使用过于简化的变分方法（如均值场近似），则会低估参数方差、忽略参数间相关性，从而给出过度自信的结果，与真实值存在偏差。这一对比验证了高级推断算法的必要性：只有充分探索和灵活近似才能正确表征复杂模型的后验分布。

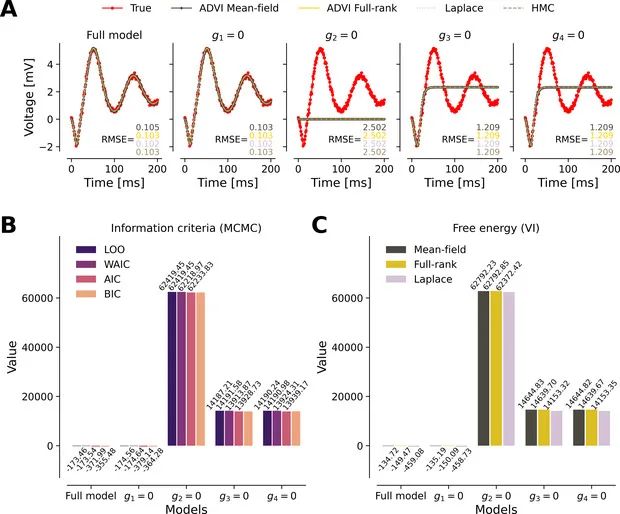
图7 模型比较。删掉哪条连接对预测影响最大。

A) 4 个删边模型的拟合曲线；B) AIC/BIC/WAIC/LOO 指标；C) 变分 Free-energy。只有删 g₁ 的模型与全模型同样好；删 g₂ 最差；指标一致给出相同排名。多种准则一致锁定了g₁ 可以为 0

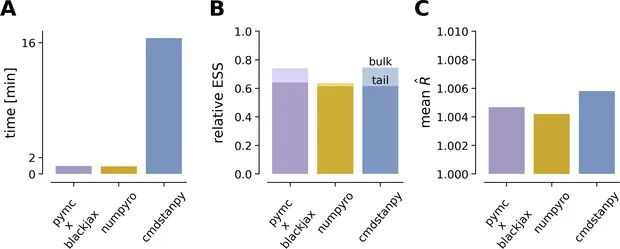
图8 PPL 性能基准。不同概率编程框架算同一模型时的速度/质量差。

A) 运行时间对比；B) ESS/抽样总量；C) 平均。NumPyro≈PyMC(BlackJAX) --> 比 Stan 快 ~16×。用 JAX 后端的 PPL（NumPyro / PyMC）既快又稳，是首选实现。

主要发现

综合而言，研究人员们在DCM模型推断的融合概率编程和贝叶斯推断，有了多重进展：

推断效率大幅提升：借助PPL框架和自动微分，高级采样算法（如NUTS）在单位时间内获取的有效样本显著增加。研究者报告相比以往手工实现的方法，新的实现方案使有效样本数/时间提高了一个数量级以上，极大缓解了采样方法“计算慢”的瓶颈。
多解不确定性得到解决：通过调优采样参数、随机初始化和结果堆叠，成功克服了后验分布的多模态问题。所有并行链几乎都能收敛到正确的全局解，推断出的参数既能良好拟合数据，又更接近生成真值。相比之下，过去的方法常常有相当比例的链陷入局部次优解，需要人工甄别。新方案令这一过程自动化完成，显著增强了推断结果的可靠性。
验证了不同推断方法的一致性：研究发现，只要算法足够得当，MCMC采样与变分推断最终可以趋同于同一个后验分布。在成功应用时，两类方法对模型证据的评估也高度一致（如全贝叶斯信息准则与自由能准则结果相符）。这为习惯于变分方法的研究者提供了信心：引入采样方法不会与既有结论相冲突，反而可以作为相互校验的工具。这种一致性也说明该DCM模型推断问题在得到充分计算支持时，其解的确定性更强。
跨平台的可复现实现：作者在多个编程平台上实现了这一DCM推断流程，并将代码开放部署在欧洲人脑计划的EBRAINS云平台上。这意味着神经成像研究者无需深厚的编程功力，也能在云端调用这些工具，对自己的数据执行自动化的DCM分析。跨平台实现还确保了结果的可重复验证，方便不同实验室采用自己熟悉的语言（如Python或C++接口）重现研究。（ https://ebrains.eu；https://github.com/ins-amu/DCM_PPLs）

DCM作为解析脑网络因果关系的强大框架，正因为推断难度高而一度令人生畏。而如今借助概率编程和先进采样技术，自动化DCM成为可能。研究人员已经在公开平台上提供了相应工具，这将让科学家以更低门槛应用DCM来分析真实的脑成像数据。例如，在研究癫痫等脑网络异常活动时，新方法可以更可靠地辨识病灶区域之间的因果影响，为临床决策提供依据；在认知神经科学中，学者们或可借此探索不同脑区对某项认知功能的因果贡献，验证假设。

更广泛来看，该研究体现了跨学科技术融合的威力。概率编程与机器学习领域的发展，正在帮助传统的生物数学模型突破计算桎梏，实现原本无法企及的推断精度。这不仅适用于脑科学，在系统生物学、生态学等涉及部分可观测非线性动力系统的领域，同样可以借鉴这样的思路改进模型分析方法。通过更灵活、精确的贝叶斯推断，我们有望在各种复杂系统中发现隐藏的因果结构和机理。

参考文献

[1] Friston, K.J. et al. (2003). Dynamic causal modelling. NeuroImage, 19(4), 1273–1302.

[2] Daunizeau, J., David, O., & Stephan, K.E. (2011). Dynamic causal modelling: A critical review of the biophysical and statistical foundations. NeuroImage, 58(2), 312–322.

[3] Frässle, S. et al. (2021). Regression dynamic causal modeling for resting-state fMRI. Human Brain Mapping, 42(7), 2159–2180.

[4] Betancourt, M. (2017). A conceptual introduction to Hamiltonian Monte Carlo. arXiv preprint arXiv:1701.02434.

[5] Vehtari, A., Gelman, A., & Gabry, J. (2017). Practical Bayesian model evaluation using leave-one-out cross-validation and WAIC. Statistics and Computing, 27(5), 1413–1432.

[6] Hoffman, M.D. & Gelman, A. (2014). The No-U-Turn Sampler: Adaptively setting path lengths in Hamiltonian Monte Carlo. J. Mach. Learn. Res., 15(1), 1593–1623.

[7] Carpenter, B. et al. (2017). Stan: A probabilistic programming language. Journal of Statistical Software, 76(1), 1–32.

[8] Phan, D. et al. (2019). Composable effects for flexible and accelerated probabilistic programming in NumPyro. arXiv preprint arXiv:1912.11554. [9] Jax team. (2022). JAX: composable transformations of Python+NumPy programs. https://github.com/google/jax

计算神经科学第三季读书会

从单个神经元的放电到全脑范围的意识涌现，理解智能的本质与演化始终是一个关于尺度的问题。更值得深思的是，无论是微观的突触可塑性、介观的皮层模块自组织，还是宏观的全局信息广播，不同尺度的动力学过程都在共同塑造着认知与意识。这说明，对心智的研究从最初就必须直面一个核心挑战：局部的神经活动如何整合为统一的体验？局域的网络连接又如何支撑灵活的智能行为？
继「神经动力学模型」与「计算神经科学」读书会后，集智俱乐部联合来自数学、物理学、生物学、神经科学和计算机的一线研究者共同发起「从神经动力学到意识：跨尺度计算、演化与涌现」读书会，跨越微观、介观与宏观的视角，探索意识与智能的跨尺度计算、演化与涌现。重点探讨物理规律与人工智能如何帮助我们认识神经动力学，以及神经活动跨尺度的计算与演化如何构建微观与宏观、结构与功能之间的桥梁。
详情请见：从神经动力学到意识：跨尺度计算、演化与涌现丨计算神经科学第三季·读书会启动