

关键词:量子游走,指数级量子加速
导 读
本文是发表于数学物理方法领域顶级期刊 Communications in Mathematical Physics 上的论文 Exponential Speedups for Quantum Walks in Random Hierarchical Graphs 的详细解读。该项工作由北京大学李彤阳课题组完成,论文的合作者包括麻省理工学院的 Shankar Balasubramanian 博士与 Aram W. Harrow 教授。
论文提出并分析了一大类具有分层结构的随机图,证明了在这类图上,量子游走的击中时间(hitting time)相对于经典算法可实现超多项式到指数级的加速;加速幅度取决于分层结构所依附的维度与随机模型。此前,量子游走在图上击中时间的指数级加速仅限于焊接树(welded tree)上。此项工作可以视作量子游走算法可以达到指数级加速的图论问题的系统性推广。

↑扫码跳转论文
论文链接:
https://link.springer.com/article/10.1007/s00220-025-05370-x
01
引 言
量子计算领域的一个核心研究方向是对哪些问题可以实现量子加速,特别是可以实现超多项式乃至指数级的量子加速。此前,达到这个级别的量子算法多来自代数与数论,以 Shor 算法为代表[1],需要明显的群论结构。
在图论中,Childs 等人[2]的工作研究了焊接树上的量子游走,是少数不依赖群结构却实现指数级量子加速的标志性结果:量子游走在多项式时间内以高成功概率到达图的出口顶点,而经典算法则需指数时间到达出口顶点。然而,该构造非常脆弱,对图结构的微扰(如短环)极为敏感,推广困难重重。
因此,量子游走是否可以对更广泛的图论问题达到超多项式乃至指数级的量子加速,是量子计算、理论计算机科学领域均十分关注的问题。
02
问题设定
我们考虑连续时间量子游走:给定无向图的邻接矩阵
我们考虑如下定义的随机分层图
首先有一个“超图”
:每个超顶点 对应一个顶点集 ,其大小为 ;
每条超边
生成 条在 与 之间的随机边(满足若干约束)。这里 , 均为事先指定的参数;
把所有超顶点/超边展开,即得实际大图
。
这一设定允许我们以结构清晰的方式,将宏观几何(如一维链、二维/三维晶格)与微观随机连接耦合起来。一个具有一维链结构分层结构的随机图如下所示。
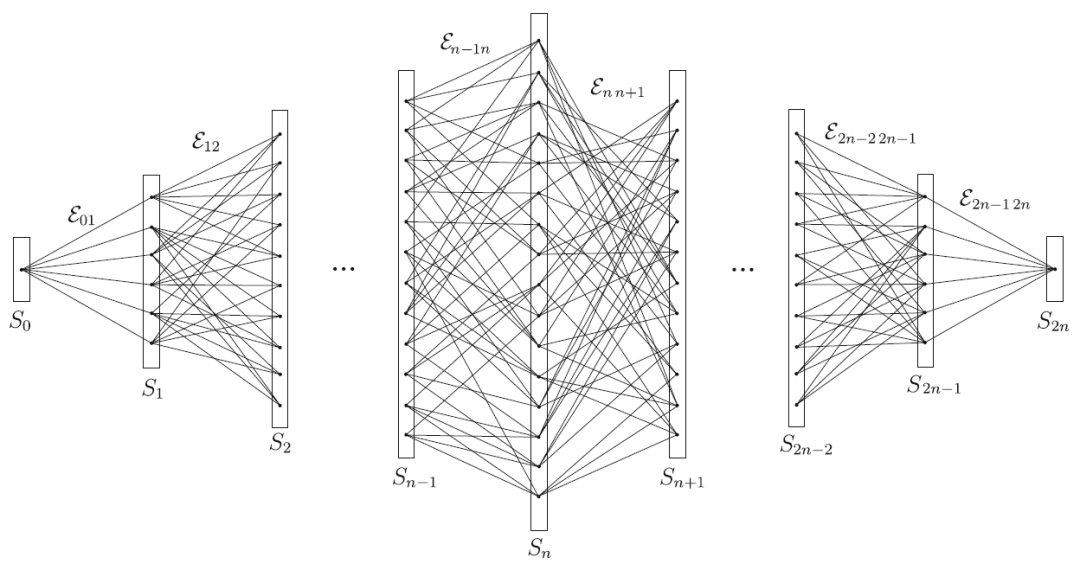
03
结 果
一维情形:超多项式加速的“常态化”
当超图
任一经典算法若要以非忽略概率从起始顶点到出口顶点,其时间至少为
;
量子游走在时间
内到达且成功率为 ,其中 与 均由一个依赖边数序列(偶-奇位点之差的对数和)的指数项乘以 为上界;
在该结果中,“焊接树”这个特例可达到指数加速,而在更通用的一维随机模型中,超多项式加速更为典型。这为过去“指数级量子加速在图论中仅是孤例”的印象提供了直观。
更高维与更一般结构:从零模到指数加速
在高维情况下,我们将超图推广到 d 维晶格上(如 Lieb 晶格[3])。我们的分析借鉴了凝聚态理论中的零能模数量与结构理论,并以此分析量子游走的可达性与速度——当零模非局域化且相干传播有效时,量子游走击中时间可达到超多项式乃至指数级量子加速。
论文的主要结果可以总结为下面的表格。
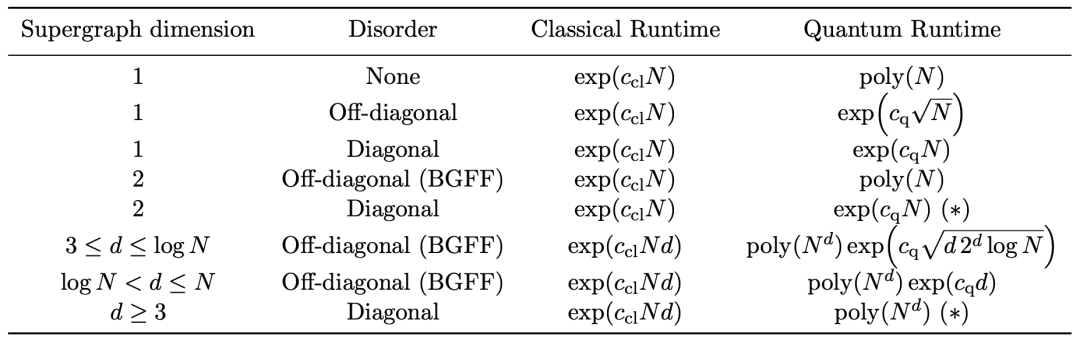
04
亮 点
(1)图稀疏化:一个可“造图”的普适方法
除晶格外,我们提出用图稀疏化在任意给定超图上构造分层图的通用方法:在相当宽的条件下,一方面经典指数下界依旧成立;而另一方面量子端的运行时间依赖所选超图的谱与态的“去局域化”(delocalization),因此当超图本征态足够扩散时,期望出现超过多项式到指数级别的量子加速。
(2)技术关键:有效维数与 Krylov 子空间
在分析上,量子游走从某个超顶点的均一叠加态出发,其动力学演化被限制在一个低维的 Krylov 子空间内;只要该子空间内的本征态不过度局域化,演化即可在较短时间内把振幅“输运”到目标位置,从而带来显著加速。
(3)物理直觉:与 Anderson 局域化的联系
在无序紧束缚模型中,Anderson 局域化[4]指出:加入随机“位能”会使本征态在空间上快速衰减,从而抑制长程输运;而在本工作构造的具有分层结构的随机图中,恰恰是零能模的(去)局域化决定了量子行走击中时间的快慢。这一点也体现在上面基于 Krylov 子空间的分析中。图论与凝聚态物理的交汇,促成了对“量子游走在什么图上更快”的可解释性刻画。
05
小结与开放性问题
本工作将焊接树指数加速这一孤例推广到一系列可系统构造、可谱分析的具有分层结构的随机图上。分析上,这项工作采用了物理化的“零模(去)局域化—Krylov 子空间”的观点。作为总结,这项工作既提供了新的范式来证明量子计算超多项式乃至指数级的量子加速,也为量子计算与凝聚态物理的交叉研究打开了可操作的通道。
本工作引出了若干值得进一步探讨的开放问题:
1) 指数 vs. 超多项式的边界:在更高维、不同随机度量与连边规则下,指数级加速的充要条件是什么?能否给出“谱—几何结构”之间的统一判据?
2)稳健性与结构扰动:当分层图中引入局部结构(如短环)时,量子加速如何退化或保持?我们的工作已指出当图具有一定程度结构时有显著的量子加速,但是更完整的答案仍需系统性研究。
3)构造性与工程化:图稀疏化流程能否导出当前量子计算实验可实现的拓扑(如在光子/超导平台上可编程实现)?怎样把“谱去局域化”的要求转译为器件层面的可控参数?
参考文献
[1] Peter W. Shor, "Algorithms for quantum computation: discrete logarithms and factoring." In Proceedings of the 35th Annual Symposium on Foundations of Computer Science, pp. 124-134. 1994.
[2] Andrew M. Childs, Richard Cleve, Enrico Deotto, Edward Farhi, Sam Gutmann, and Daniel A. Spielman. "Exponential algorithmic speedup by a quantum walk." In Proceedings of the 36th Annual ACM Symposium on Theory of Computing, pp. 59-68. 2003.
[3] Elliott H. Lieb. "Two theorems on the Hubbard model." Physical Review Letters 62, no. 10 (1989): 1201.
[4] Philip W. Anderson. "Absence of diffusion in certain random lattices." Physical Review 109, no. 5 (1958): 1492.

图文 | 李彤阳
PKU QUARK Lab
关于量子算法实验室
量子算法实验室 QUARK Lab (Laboratory for Quantum Algorithms: Theory and Practice) 由李彤阳博士于2021年创立。该实验室专注于研究量子计算机上的算法,主要探讨机器学习、优化、统计学、数论、图论等方向的量子算法及其相对于经典计算的量子加速;也包括近期 NISQ (Noisy, Intermediate-Scale Quantum Computers) 量子计算机上的量子算法。
实验室新闻:#PKU QUARK
实验室公众号:
课题组近期动态


— 版权声明 —
本微信公众号所有内容,由北京大学前沿计算研究中心微信自身创作、收集的文字、图片和音视频资料,版权属北京大学前沿计算研究中心微信所有;从公开渠道收集、整理及授权转载的文字、图片和音视频资料,版权属原作者。本公众号内容原作者如不愿意在本号刊登内容,请及时通知本号,予以删除。

点击“阅读原文”转论文链接
内容中包含的图片若涉及版权问题,请及时与我们联系删除



评论
沙发等你来抢