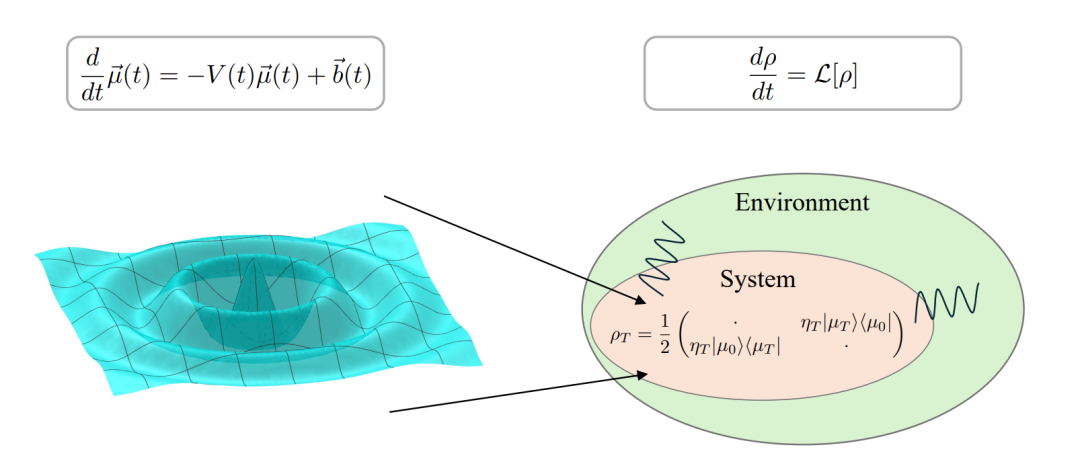
港大联合团队创新性引入“非对角密度矩阵编码”技术，为量子计算在科学计算中的应用开辟新路径

“ 导语：在科学与工程领域，从流体力学到量子物理，许多复杂系统的建模都离不开线性微分方程组。对于高维问题，即使使用超级计算机，传统算法也常面临计算瓶颈。量子计算以其原理上的并行性，被视为解决该类问题的潜在途径。然而，一个根本性挑战在于：如何让本质上遵循幺正演化（信息与能量守恒）的量子计算机，有效模拟现实世界中普遍存在的非幺正（耗散或增益）动力学过程。”



近日，由香港大学、北京大学和新加坡国立大学研究人员组成的团队，在该领域取得重要进展。他们提出了一种全新的量子算法，通过巧妙地利用开放量子系统的自然耗散特性来求解线性微分方程。理论分析表明，该算法在多个关键参数上的效率达到了“近乎最优”，超越了现有方案。相关论文《Designing a nearly optimal quantum algorithm for linear differential equations via Lindbladians》已发表于物理学顶级杂志《Physical Review Letters》。





01

—


核心挑战：非幺正动力学的量子嵌入



求解线性微分方程是量子计算有望展现优势的应用场景之一。其挑战根源在于，描述大多数物理过程的微分方程，其系数矩阵通常为非厄米矩阵，导致时间演化算符是非幺正的。这意味着系统可能存在能量耗散或增益。

然而，量子计算机的硬件运行基于幺正演化。此前的主流量子算法，或通过复杂的线性系统求解间接处理，或通过“块编码”将非幺正算符嵌入一个更大的幺正算符的子空间中。这些方法如同“翻译”过程，虽能解决问题，但往往会引入额外的计算开销，使得算法效率未能达到理论预期的最优水平。


02

—


创新路径：从“对抗耗散”到“利用耗散”



面对这一困境，研究团队转换了思路——与其设法在封闭系统中“模拟”耗散，不如直接利用开放量子系统固有的非幺正动力学。
他们引入了名为 “非对角密度矩阵编码” 的核心技术。该技术将微分方程的解，编码在一个辅助量子比特与系统耦合所形成的密度矩阵的非对角块中。这一做法巧妙地绕过了密度矩阵本身需为厄米正定的限制，从而能够通用地编码任意线性微分方程的解。
基于此编码方案，研究者构建了一个对应的林布拉德方程。该方程描述了一个量子系统与环境的相互作用。其中，微分方程系数矩阵的反对称（振荡）部分被映射为系统的内部哈密顿量，而对称（耗散）部分则自然地由环境引入的量子跳跃算符所描述。
通过这种方式，目标微分方程的求解过程，被精确地转化为一个开放量子系统的自然演化。演化结束时，其解即存储在末态密度矩阵的特定位置，可通过进一步的量子测量或幅度放大技术提取。



03

—


算法性能：在关键指标上实现近乎最优



研究团队对算法复杂度进行了详细分析，并与现有量子算法进行了全面对比。
结果表明，在一种更为自然的“平方根输入模型”下，新算法在三个关键参数——模拟时长T、解的范数η_T 和精度ε——上的依赖关系，均达到了已知的理论下界，即实现了“近乎最优”。
具体而言，算法对初始态制备的查询复杂度为最优的O(ηₜ⁻¹)。同时，其对问题矩阵的查询复杂度为Õ(ηₜ⁻¹αᴠ T log(1/ε) / log log(1/ε))，在时间T上实现了线性依赖，优于部分算法的二次依赖，且在误差ε上的依赖也达到了理论极限。


04

—


应用前景：超越微分方程求解的启示



这项工作的意义不仅在于提供了一个高效的微分方程量子解法。
  • 为非厄米物理研究提供新工具：许多非厄米物理系统的动力学可直接由线性微分方程描述。该算法使得在量子计算机上精确模拟这类系统的长时间演化成为可能，为研究诸如奇异点、非厄米趋肤效应等新颖物理现象提供了新平台。
  • 应用于量子热态制备：研究显示，该算法可直接用于高效制备吉布斯态和估算配分函数，这是量子模拟和量子化学中的核心任务。
  • 启发算法设计新范式：这项工作成功地将量子计算中“利用物理系统固有特性解决计算问题”的理念付诸实践，通过林布拉德方程这一非幺正动力学模型，实现了对另一类非幺正问题（微分方程）的最优求解，为未来解决更多数值计算问题开辟了新的思路。
“我们的工作表明，开放量子系统不仅是需要被模拟的对象，其丰富的动力学本身也可以成为进行量子计算的资源。”论文作者表示，“这为探索量子计算在更广泛科学计算场景中的应用提供了新的可能性。”



论文信息：

Zhong-Xia Shang, Naixu Guo, Dong An, Qi Zhao. "Design nearly optimal quantum algorithm for linear differential equations via Lindbladians." Phys. Rev. Lett. 135, 120604 (https://journals.aps.org/prl/abstract/10.1103/cvl9-97qg) 


术语解释：

  • 线性微分方程：描述未知函数及其导数之间线性关系的方程，是科学建模的基础工具。

  • 量子算法：在量子计算机上运行的算法，利用量子力学特性如叠加和纠缠，以加速计算。

  • 开放量子系统：与外部环境存在相互作用的量子系统。

  • 林布拉德方程：描述开放量子系统在马尔可夫近似下动力学的主流方程。

  • 非对角密度矩阵编码：本工作提出的新技术，将目标信息编码在密度矩阵的非对角元中。

  • 近乎最优：算法复杂度与理论证明的复杂度下界非常接近。

内容中包含的图片若涉及版权问题，请及时与我们联系删除