NeurIPS 2025 | 利用物理信息神经网络加速大规模变分量子算法

关键词：量子计算，变分量子算法，物理信息神经网络

导读

本文是对发表于计算机人工智能领域顶级会议 NeurIPS 2025 的论文 PALQO: Physics-informed Model for Accelerating Large-scale Quantum Optimization 的解读。该工作由北京大学袁骁课题组与电子科技大学、南洋理工大学、复旦大学合作完成，论文共同第一作者为北京大学计算机学院博士后黄一鸣和电子科技大学博士生郝亚杰。

该工作提出了一种基于物理信息神经网络的变分量子算法高效训练方案，为提升近中期量子设备的实用化提供了新思路。针对不可克隆定理导致无法使用标准反向传播、从而造成大规模任务量子资源开销过高的问题，该方法将 VQA 训练动力学重构为非线性偏微分方程，并利用物理信息神经网络对其进行高效建模。该方案通过少量量子采样数据在经典侧预测多步参数更新，显著降低量子资源消耗。

论文地址：

https://arxiv.org/abs/2509.20733

问题与背景

变分量子算法是一类结合量子计算与经典优化的混合算法，通过参数化量子线路生成量子态，并利用经典优化器迭代更新参数，以求解量子系统的基态能量或执行特定机器学习与优化任务。为推动变分量子算法在大规模问题上的发展，研究者们已在提升其优化效率方面投入了大量努力。现有相关研究大致可分为三类。第一类方法通过对哈密顿量项进行分组，实现多项同时测量，从而降低量子多体与量子化学问题中的测量成本^[1,2]。第二类方法利用经典模拟器或学习模型，为给定的 VQA 寻找接近损失函数局部极小值的优良初始参数，从而加速收敛^[3,4,5]。第三类方法则通过修正已有的优化轨迹预测参数更新动态，典型代表包括循环神经网络^[6]与 QuACK 方法^[7]。尽管上述方向取得了显著进展，但在大规模任务中，现有方法仍难以在优化效率与精度之间实现有效平衡。由此，一个关键问题随之产生：对于大规模 VQA 系统，是否有可能同时兼顾两者？

解决方法

针对这一问题，我们注意到以往研究主要集中于硬件改进与启发式优化，而通过近似训练动力学以缓解量子资源负担的潜力尚未得到充分探索。为此，我们提出了一种全新的视角：利用泰勒展开将变分量子算法的参数优化过程重新表述为一个非线性偏微分方程，其中该方程的演化对应于训练过程中参数更新的轨迹，即 $\frac{\partial \boldsymbol{\theta}}{\partial t} = -\frac{\partial{\mathcal{E}}}{\partial \boldsymbol{\theta}},$ 以及 $\frac{\partial \mathcal{E}}{\partial t}=-\sum_{i}\left(\frac{\partial \mathcal{E}}{\partial \boldsymbol{\theta}_{i}}\right)^{2}+\frac{\eta}{2} \sum_{j, k} \frac{\partial^{2} \mathcal{E}}{\partial \boldsymbol{\theta}_{j} \partial \boldsymbol{\theta}_{k}} \frac{\partial \mathcal{E}}{\partial \boldsymbol{\theta}_{j}} \frac{\partial \mathcal{E}}{\partial \boldsymbol{\theta}_{k}}+\mathcal{O}\left(\eta^{2}\right),$ 其中， $\boldsymbol{\theta}$ 是变分量子算法中的参数， $\mathcal{E}$ 是能量函数。

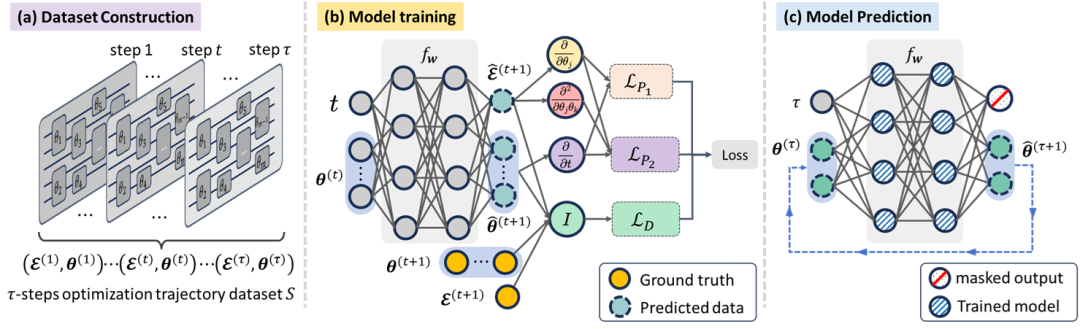
基于这一理论框架，我们设计了一种名为 PALQO 的方案，借助物理信息神经网络^[8]近似求解该 PDE。方案的整体流程下图所示，包括三个阶段：数据集构建、模型训练与模型预测。首先如图(a)所示生成数据集 $\mathcal{S} = \{\boldsymbol{\theta}^{(t)}, \mathcal{E}^{(t)}\}_{t=1}^\tau$ ，该数据集对应量子设备在 $\tau$ 次优化步骤中采集的参数轨迹 $\boldsymbol{\theta}$ 及能量损失 $\mathcal{E}$ 。接着，图(b)所示，PALQO 利用收集的 $\mathcal{S}$ 训练基于 PINN 的模型 $f{\boldsymbol{w}}$ ，以捕捉潜在的优化动力学。获得训练好的 $f{\boldsymbol{w^*}}$ 后，如图(c)所示，该模型可递归预测未来步骤的参数 $\boldsymbol{\theta}$ ，直至收敛，即满足 $|\boldsymbol{\theta}^{(t)} - \boldsymbol{\theta}^{(t+1)}| + |\mathcal{E}^{(t)} - \mathcal{E}^{(t+1)}|\leq \varsigma,$ 其中 $\varsigma$ 为一个小常数。直接进行长期预测以达到目标问题的最优解是极其困难的。为此，我们采用不重叠滑动窗口的方法来增强网络的长期预测能力。

根据参数优化过程的非线性偏微分方程表述，我们将其视为物理约束并构建了如下代价函数： $\mathcal{L} = \lambda_D \mathcal{L}_D + \lambda_{P_1} \mathcal{L}_{P_1} + \lambda_{P_2} \mathcal{L}_{P_2},$ 其中，
$\begin{array}\ \mathcal{L}_D = \sum_{t=1}^\tau \Big(\mathcal{E}^{(t)} - \hat{\mathcal{E}}^{(t)}\Big)^2+\sum_{t=1}^\tau \Big( \boldsymbol{\theta}^{(t)} - \hat{\boldsymbol{\theta}}^{(t)}\Big)^2,\\ \mathcal{L}_{P_1}=\sum_{t=1}^\tau \Big(\sum_{j=1}^p (\frac{\partial \hat{\boldsymbol{\theta}}^{(t)}_j}{\partial t} + \frac{\partial \hat{\mathcal{E}}^{(t)} }{\partial \boldsymbol{\theta}^{(t)}_j } )\Big)^2,\\ \mathcal{L}_{P_2}=\sum_{t=1}^\tau\Big(\frac{\partial \hat{\mathcal{E}}^{(t)}}{\partial t}+\sum_{j=1}^p \Big(\frac{\partial \hat{\mathcal{E}}^{(t)}}{\partial \boldsymbol{\theta}^{(t)}_j}\Big)^2 - \frac{\eta}{2}\sum_{j,k=1}^p \frac{\partial^2 \hat{\mathcal{E}}^{(t)}}{\partial \boldsymbol{\theta}^{(t)}_j\partial \boldsymbol{\theta}^{(t)}_k} \frac{\partial \hat{\mathcal{E}}^{(t)}}{\partial \boldsymbol{\theta}^{(t)}_j}\frac{\partial \hat{\mathcal{E}}^{(t)}}{\partial \boldsymbol{\theta}^{(t)}_k}\Big)^2. \end{array}$

理论结果

若 PALQO 的物理信息神经网络由 $L$ 层 tanh 神经网络构成，每层最大宽度为 $W$ ，将其在 $\tau$ 个训练样本上进行训练，来近似具有 $p$ 个可调参数 $\boldsymbol{\theta}$ 的变分量子本征求解器训练动力学对应的偏微分方程解。则有至少 $1-\gamma$ 的概率，其泛化误差可被上界为 $\tilde{\mathcal{O}}\left(\sqrt{\frac{pL^2W^2}{\tau}\left(\ln\left(\frac{p}{\epsilon}\right)+\ln\left(\frac{1}{\gamma}\right)\right)}\right).$ 结果表明，对于任意 $\epsilon>0$ ，训练样本数量最多仅需以 $p$ 、 $L$ 和 $W$ 的多项式规模增长，即可保证泛化误差有界。这保证了 PALQO 在大规模场景中的适用性。

数值实验

为了评估所提出的 PALQO 框架的实际性能，我们将其应用于两个具有代表性的量子任务：估计多体量子系统（横场伊辛模型 TFIM、海森堡模型 HQ）的基态能量及量子化学中分子（BeH₂）的基态能量。

量子测量的开销对比

我们将优化过程中所需的测量次数作为量子资源的度量，用以评估 PALQO 及其他基准模型在不同任务中的性能，包括：采用 HEA 电路的20量子比特横场伊辛模型（TFIM）、采用 HVA 电路的20量子比特海森堡模型，以及采用 UCCSD 变分波函数的14量子比特 BeH₂ 分子系统。PALQO 在任务中实现了资源消耗的显著降低。在能量误差保持在约 $10^{-3}$ 的水平下，平均测量开销降低约90%。

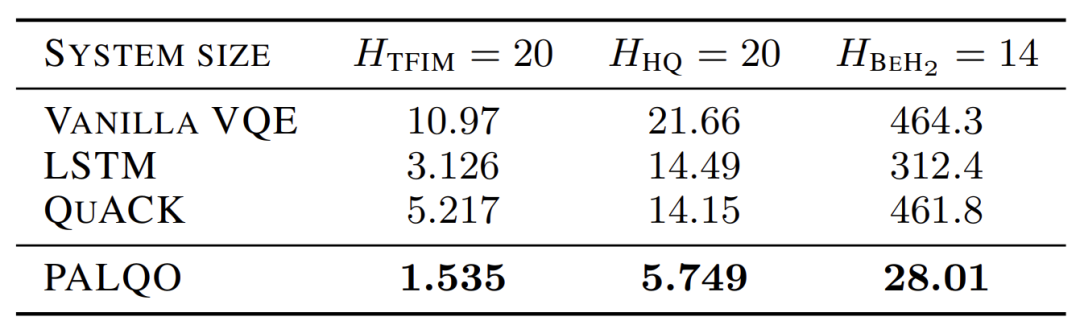
表1. TFIM 模型、海森堡模型以及 BeH₂ 所需的量子测量次数对比

精度和效率上的对比

我们分别对比了 PALQO 在不同任务中的性能，包括采用 HEA 变分线路20量子比特的横场伊辛模型（TFIM）、采用采用 HVA 变分线路20量子比特的海森堡模型（Heisenberg），以及采用 UCCSD 变分线路14量子比特的 BeH₂ 分子。

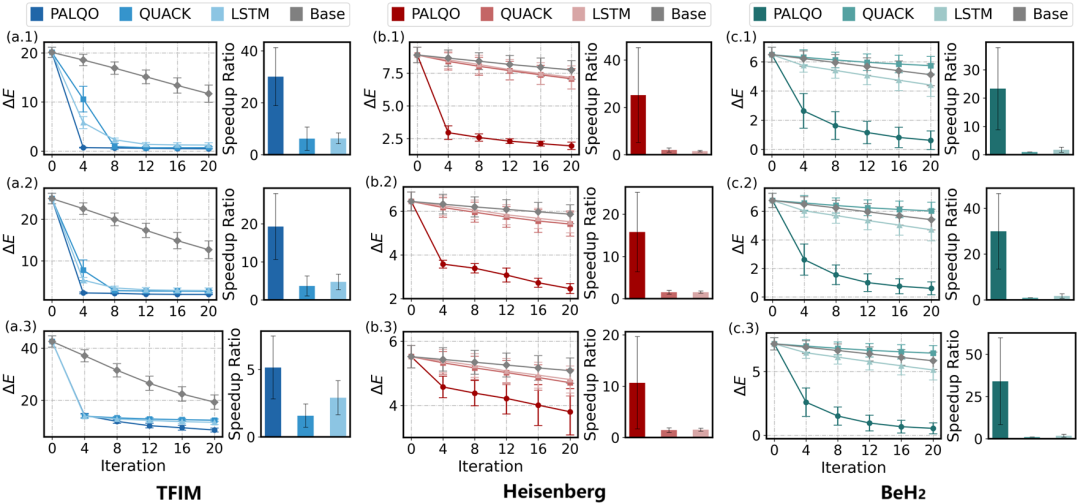
每个子图包含在量子设备上迭代得到的 $\Delta E$ 曲线，以及显示 PALQO 与其他对比模型加速比的柱状图。左列展示了横场伊辛模型（TFIM）下 $J/h=\{2,1,0.5\}$ 的结果；中列展示了海森堡模型下 $J_x=J_y=h=1, J_z=\{0.5,1,2\}$ 的结果；右列展示了 BeH₂ 分子在键长 $b=\{1.3,1.4,1.5\}$ 下的模型性能。

相比于其他方法，PALQO 始终表现优异，例如在横场伊辛模型（TFIM， $J/h=2$ ）配合 HEA 量子态构型的情况下，实现了最高约30倍的加速，同时能量误差 $\Delta E =|\hat{E} - E|$ 控制在约 $10^{-3}$ 量级。

可扩展性

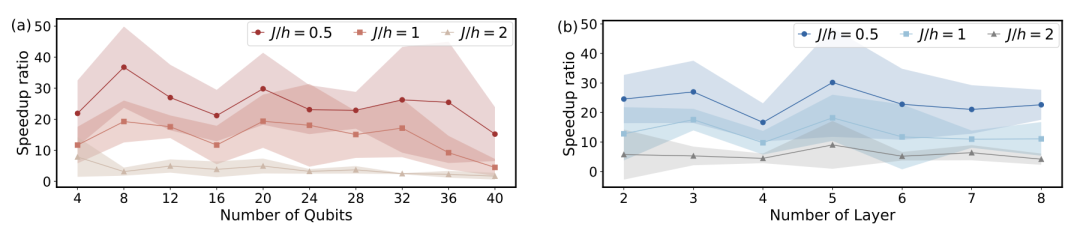
此外，我们在横场伊辛模型（TFIM）HEA 线路上研究 PALQO 的可扩展性，考察其在系统规模（从 $n=4$ -qubits 到 $n=40$ -qubits）和线路层数（从2到8）增加时的性能表现。如下图所示，结果表明 PALQO 均具有加速表现，但效果依赖于具体的系统配置。

如图(a)所示，尽管随量子比特数量变化，加速比存在波动，但在 $J/h=0.5$ 时仍可实现最高约30倍的加速。当 $J/h=2$ 时，加速较低，这是由于基态与第一激发态之间能隙较小，使优化更具挑战性。类似的情况也出现在图(b)中。这表明，随着系统大小、计算需求的增加，PALQO 的性能优势仍能保持，显示了其在大规模量子优化中的潜力。

参考文献

[1] Vladyslav Verteletskyi, Tzu-Ching Yen, and Artur F Izmaylov. Measurement optimization in the variational quantum eigensolver using a minimum clique cover. The Journal of chemical physics, 152(12), 2020.

[2] Tzu-Ching Yen, Aadithya Ganeshram, and Artur F Izmaylov. Deterministic improvements of quantum measurements with grouping of compatible operators, non-local transformations, and covariance estimates. npj Quantum Information, 9(1):14, 2023.

[3] Alexey Galda, Xiaoyuan Liu, Danylo Lykov, Yuri Alexeev, and Ilya Safro. Transferability of optimal qaoa parameters between random graphs. In 2021 IEEE International Conference on Quantum Computing and Engineering (QCE), pages 171–180. IEEE, 2021.

[4] Shikun Zhang, Zheng Qin, Yongyou Zhang, Yang Zhou, Rui Li, Chunxiao Du, and Zhisong Xiao. Diffusion-enhanced optimization of variational quantum eigensolver for general hamiltonians. arXiv preprint arXiv:2501.05666, 2025.

[5] Ricard Puig, Marc Drudis, Supanut Thanasilp, and Zoë Holmes. Variational quantum simulation: A case study for understanding warm starts. PRX Quantum, 6:010317, Jan 2025. doi: 10.1103/PRXQuantum.6.010317. URL https://link.aps.org/doi/10.1103/ PRXQuantum.6.010317.

[6] Guillaume Verdon, Michael Broughton, Jarrod R McClean, Kevin J Sung, Ryan Babbush, Zhang Jiang, Hartmut Neven, and Masoud Mohseni. Learning to learn with quantum neural networks via classical neural networks. arXiv preprint arXiv:1907.05415, 2019.

[7] Di Luo, Jiayu Shen, Rumen Dangovski, and Marin Soljacic. Quack: accelerating gradientbased quantum optimization with koopman operator learning. Advances in Neural Information Processing Systems, 36, 2024.

[8] Maziar Raissi, Paris Perdikaris, and George E Karniadakis. Physics-informed neural networks: A deep learning framework for solving forward and inverse problems involving nonlinear partial differential equations. Journal of Computational physics, 378:686–707, 2019.

图文 | 黄一鸣

PKU Qtheory Group

量子模拟和量子信息实验室

Quantum Simulation and Quantum Information Lab

量子模拟和量子信息实验室由袁骁博士于2020年创立。该实验室的研究方向包括量子算法设计、量子机器学习、量子计算实验。

The Quantum Simulation and Quantum Information Lab was founded by Dr. Xiao Yuan in 2020 at Peking University, focusing on quantum simulation and computing algorithms and quantum information theory. We are currently focusing on three research directions:

Quantum computing

Quantum algorithms for NISQ and universal quantum computers
Quantum error mitigation and quantum error correction
Quantum computing for realistic problems

Quantum machine learning

Applying machine learning in quantum computing
Enhancing machine learning leveraging quantum computing

Quantum experiment

Efficient benchmarking and calibration of quantum hardware
Experimental implementation of quantum algorithms

实验室 PI：袁骁助理教授

实验室相关新闻：#PKU Qtheory

实验室公众号：

Qtheory近期动态

本微信公众号所有内容，由北京大学前沿计算研究中心微信自身创作、收集的文字、图片和音视频资料，版权属北京大学前沿计算研究中心微信所有；从公开渠道收集、整理及授权转载的文字、图片和音视频资料，版权属原作者。本公众号内容原作者如不愿意在本号刊登内容，请及时通知本号，予以删除。

点击“阅读原文”转论文链接

内容中包含的图片若涉及版权问题，请及时与我们联系删除

NeurIPS 2025 | 利用物理信息神经网络加速大规模变分量子算法

评论列表

评论