henry 发自 凹非寺
量子位 | 公众号 QbitAI
在谷歌发布Gemini 3 Deep Think爆火后,OpenAI也开始放出新的能力信号。
刚刚,OpenAI表示:他们用尚未发布的内部模型,在一周内尝试解答10道来自数学家科研现场的真实问题,其中有5道被认为基本正确。
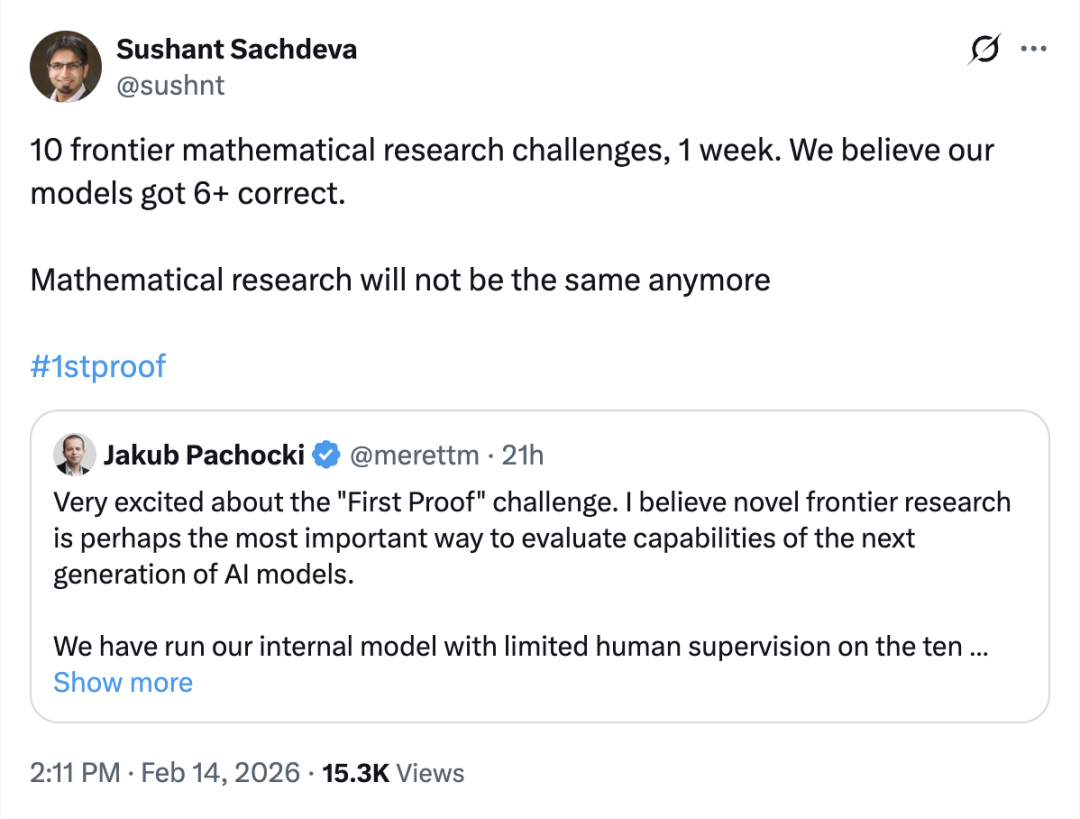
值得一提的是,这批题目与此前GPT、Gemini等模型在IMO类测试中取得金牌成绩时面对的题目完全不同。
它们不来自标准题库,也不是竞赛题,而是直接取自数学家真实研究过程中的自然问题。
这在很大程度上切断了模型“背答案”或通过训练数据污染获得优势的可能性,从而意味着模型自主推理能力再次进化。
正如一位网友所说:
这里最聪明的地方,是把答案公开,但用加密的方式保存。这基本解决了困扰其他benchmark的老问题,模型是不是从训练数据里记住了答案。
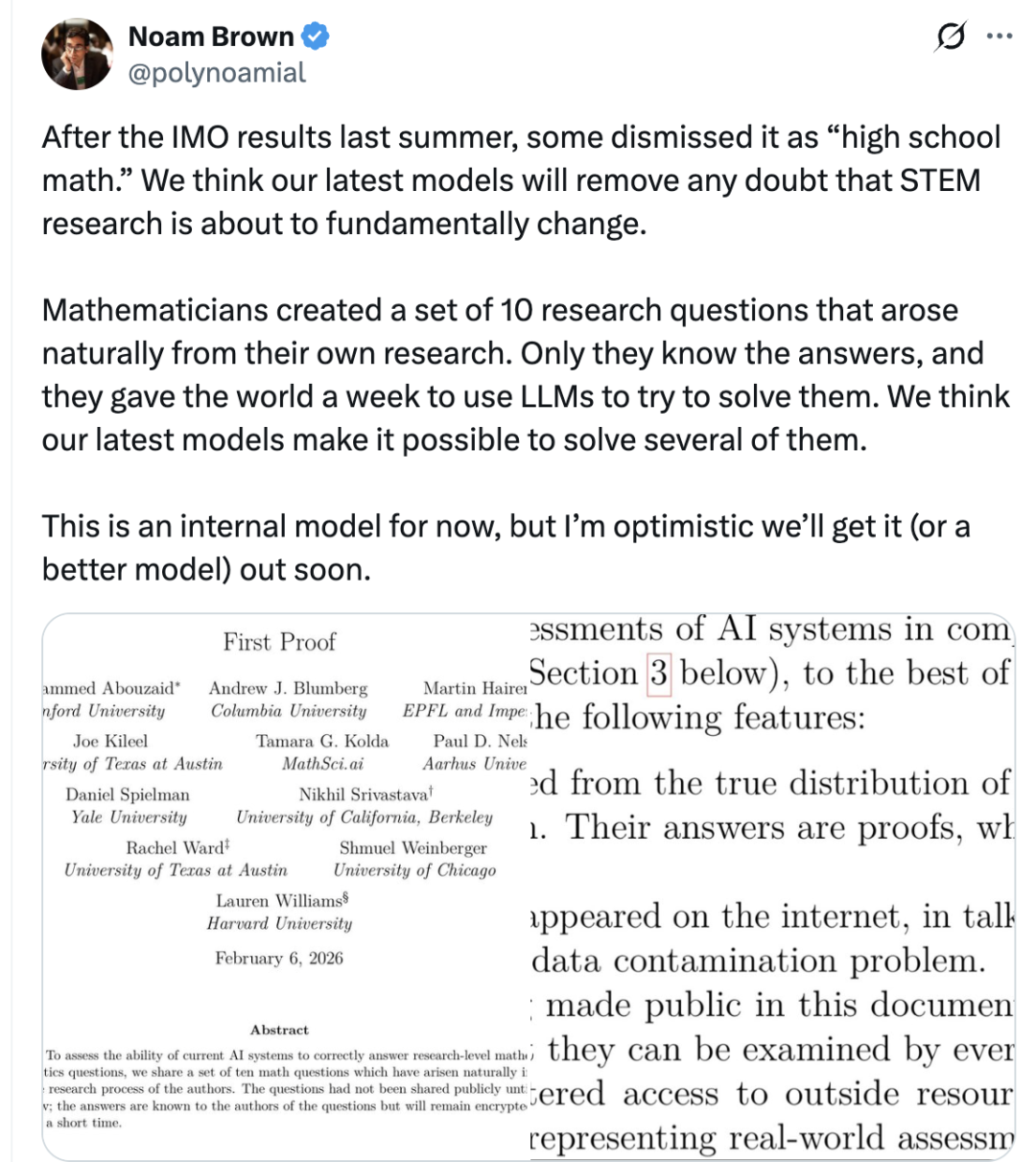
此外,据称OpenAI研究员,o1核心贡献者Noam Brown表示:
这款内部模型很快就要发布了。
解决一半的真实数学问题
相信眼尖的你已经发现了:为什么图片里写的是6道,但正文却说是5道?
在早期评估中,确实一度认为模型做对了6道。
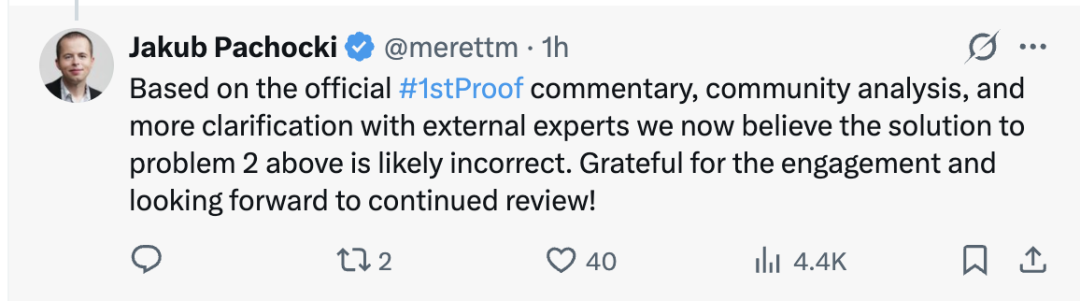
但随后在社区讨论与复核反馈中,第2题的解法被指出可能存在问题。
根据OpenAI的Jakub Pachocki的说法,第2题很可能是错的,因此更保守的估计应该在5道左右。
至于具体做对了哪些题,咱们先看这次测试本身是如何进行的。
OpenAI方面表示,这只是一次为期一周的侧向冲刺:
主要通过查询他们当前正在训练的模型来完成,因此方法论上仍有不少局限。
在评估过程中,他们没有向模型提供证明思路或数学提示。
对于部分解答,只是在专家反馈后要求模型进一步展开证明细节。
同时,团队还人工协调该模型与ChatGPT之间的往返交流,用于验证、格式整理与风格调整。
对于个别问题,最终呈现的版本是基于人工判断,从多次尝试中挑选出的最佳结果。
在下面的10道题中,OpenAI的内部模型在第4、5、6、9、10题上给出了较为可靠的答案。

接下来,我们具体来看。
4.有限加性卷积与Φₙ的调和平均不等式
问题:给定两个n次首一实根多项式p和q,定义一种特殊的卷积运算。
需要证明:反映根部拥挤程度的指标(根间距离倒数平方和)的倒数,在卷积后满足调和平均不等式。本质是在探究该运算是否会让根分布更加均匀。

模型给出的思路是:
特征转化:利用残留公式将指标转化为一组正数的倒数和。
矩阵分解:证明卷积后的权重向量可表示为原向量的加权组合,权重矩阵具双随机结构。
不等式放缩:通过Jensen不等式与凸性分析推出稳定性指标提升
5. O-适配切片滤过与切片连通性的几何不动点判据
问题:G-等变稳定范畴中,由N∞算子诱导的切片过滤结构。
模型给出的思路是:
结构定义:利用由群表示生成的切片单元构造局部化子范畴,从而建立对应的切片过滤层级框架。
判据建立:证明一个连通G-谱属于某一层级,当且仅当对所有子群取几何定点后,其连通性满足相应阈值条件,从整体结构转化为局部检测问题。
证明路径:通过各向同性分离方法进行归纳推导,并结合双陪集公式处理诱导谱的几何定点,将问题最终化简为几何定点检测的等价判定。
6.大规模 ε-轻顶点子集
第六题研究图论中ε-轻子集(ε-light subset) 的存在性。
若子集诱导拉普拉斯算子的能量始终不超过整图ε倍,则称其为ε-轻。
需证明:是否存在常数c,使任意图都能找到规模至少cε|V|的此类子集。
模型给出的思路是:
线性代数转化:将问题重写为矩阵不等式约束:在拉普拉斯算子的值域中寻找顶点集合,使其边贡献矩阵之和受上界控制。
部分着色构造:使用约16/ϵ种颜色,对约四分之一顶点进行贪心着色,为后续筛选结构提供候选划分。
屏障函数控制:引入源自谱稀疏化理论的屏障方法,通过控制潜在函数保证每次选择顶点与颜色时矩阵增长保持可控,从而维持不等式约束。
子集提取:着色结束后利用鸽巢原理选取最大颜色类作为S,并证明该集合满足 ε-轻性质,且规模下界为ε|V| / 256,从而得到存在性结论,给出常数c=1/256。
9.缩放四线性行列式张量之间的代数关系
问题:给定若干矩阵构造四阶张量,目标是用多项式映射判定系数是否可分解为四向量外积。
模型给出的思路是:
张量封装:将所有输入张量重新排列并合并为一个大张量,使问题转化为单个高维对象的结构判定。
构造映射:定义F为该张量在四个维度展开(flattening)后所得矩阵的所有5×5子式。这些子式本身即为次数为 5 的多项式函数。
秩约束证明:证明若系数具有分解结构,则对应展开矩阵秩不超过4,因此所有5×5子式必然为零,从而满足映射条件。
必要性验证:在Zariski泛性假设下,证明子式全部消失反过来也蕴含矩阵秩受限,从而恢复单模态分解结构,最终得到整体分解形式成立。
10.含缺失数据的核化 CP–ALS 子问题:基于 Kronecker 预条件的无矩阵 PCG 方法
问题:CP分解下,线性系统规模巨大。问题在于如何避免显式构造矩阵。
模型给出的思路是:
矩阵自由算子:利用观测索引集合Ω与Kronecker结构,将矩阵乘向量操作改写为仅针对已观测条目的收缩计算。通过直接作用于对应因子行与选择矩阵,实现线性算子的应用,避免构造完整系数矩阵。
Kronecker预条件子:针对采样不均匀带来的收敛困难,构造结构接近原算子的预条件子。该结构能够压缩谱分布,显著提升迭代收敛速度。
快速求逆应用:对核矩阵与Gram矩阵做特征分解,并利用Kronecker可分结构,将预条件子的逆作用化为低成本的基变换与对角缩放操作。
First Proof测试是什么?
这上面的5道题,均来自1st Proof项目。
对应问题的解答文件已于2月13日发布,而模型测试是在正式发布前一周完成的。
(注:解答文件包括作者解答、原始加密答案、项目团队生成的AI解答)
需要强调的是,这些问题本身仍处在持续讨论与研究阶段,因此模型给出的结果并不存在所谓“标准答案”。
是否正确、价值几何,都需要领域专家与社区进一步评估。
也正因此,社区验证不同解题路径成为过程的一部分——
像第2题这样,最初看似成立、后来被指出问题的情况,也在意料之内。
那么,1st Proof到底是什么?
简单来说,这是一个面向AI能力评估的实验性项目,其核心目标很直接:
用真实科研过程中自然产生的数学问题,测试AI是否能够自主完成研究级证明。

项目首轮发布了一组10道研究级数学问题,用来评估AI系统在接近真实科研环境下的能力表现。
这些问题涵盖代数组合、谱图论、代数拓扑、随机分析、辛几何、表示论、李群格点、张量分析、数值线性代数等多个数学方向。
它们都来自作者自身研究过程,并且理论上可在约5页证明内解决(答案最初未公开)。
据悉,下一轮问题设计细节预计在今年3月14日公布。
问题发布后,不少研究者也参与到模型答案的验证之中。
比如,CMU助理教授Yang Liu就在社交媒体上详细讨论了第六题。
他表示OpenAI的解答基本正确,并直言当前模型在数学能力上的进步令人印象深刻。

更具体地说,他指出:
当前模型已经相当擅长证明那类自包含的问题陈述——尤其是当解法建立在已有文献思想之上,或证明本身较为简短时。
在他看来,这一框架很好地捕捉了两个方向的进展:
一端是IMO/竞赛数学,另一端则是更贴近研究环境的数学推理能力。
与此同时,也有不少讨论认为:
如果大语言模型能够处理原创性的数学问题,那么我们或许很快就会看到AI不只是解题,而是开始产生新的洞见——这将成为STEM研究领域的一个颠覆性转折点。

事实上,像1st Proof这样的测试集本身就体现了评估思路的变化。
正如一位网友所说,这次值得关注的,并不是ChatGPT或Gemini的表现,而是测试设计本身:
由11位数学家构建的高难度问题集,直接取自未发表研究;它们无法通过检索获得答案,只能依赖推理与构造。在这样的设定下,即便公开版本模型表现有限,内部模型仍能正确解决10题中的至少 6 题,这件事真正引发讨论的点,也就不在“成绩”,而在能力形态。
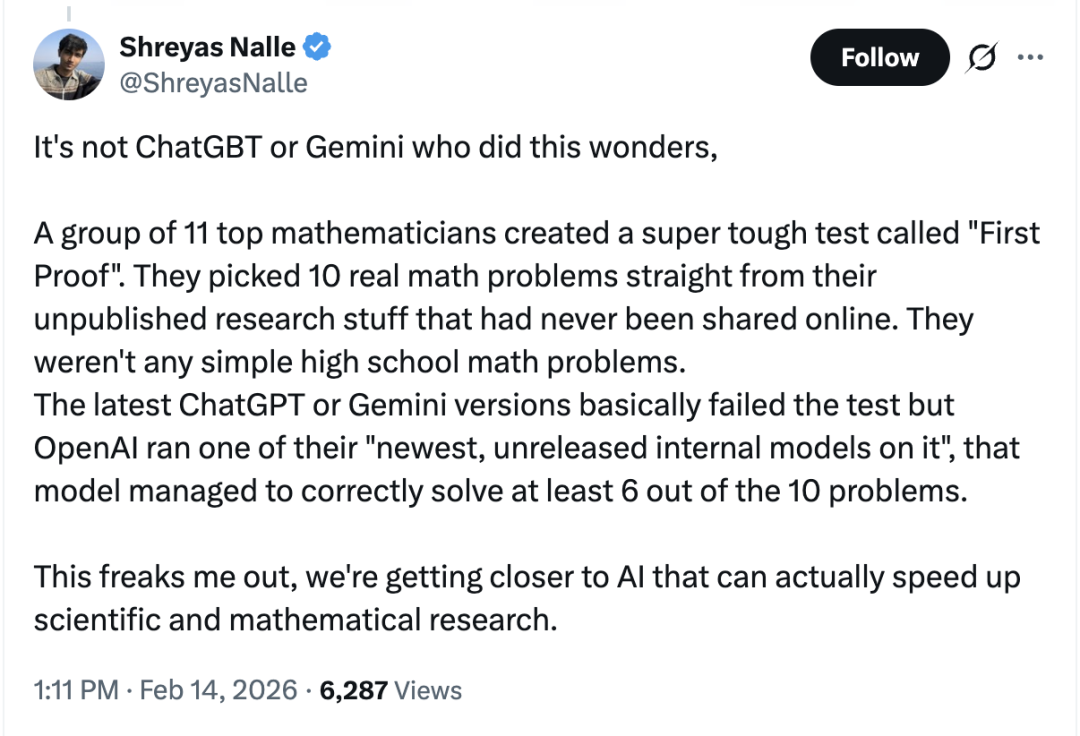
因为关键变化是:当模型面对无法背诵答案的问题,仍能产出被专家认真评估的证明路径时,它展现出的行为更接近自主推理,而非知识回放。
这释放了两个信号:
一方面OpenAI 内部模型的数学推理能力,正在逼近研究级问题空间。
另一方面,评测范式正在改变——
不再只是用题库刷新分数,而是开始把模型放进科研现场,用真实问题检验其思考能力。
参考链接:
[1]https://x.com/polynoamial/status/2022527227049742779
[2]https://1stproof.org/
[3]https://cdn.openai.com/pdf/a430f16e-08c6-49c7-9ed0-ce5368b71d3c/1stproof_oai.pdf
— 欢迎AI产品从业者共建 —

一键关注 👇 点亮星标
内容中包含的图片若涉及版权问题,请及时与我们联系删除



评论
沙发等你来抢