【论文标题】Reinforced Few-Shot Acquisition Function Learning for Bayesian Optimization
【作者团队】Bing-Jing Hsieh, Ping-Chun Hsieh, Xi Liu
【发表时间】2021/06/08
【机 构】台湾新竹,国立交通大学,计算机科学系
【论文链接】https://arxiv.org/pdf/2106.04335.pdf
【推荐理由】本文出自台湾新竹国立交通大学,本文旨在通过强化少样本 AF 学习 (FSAF) 的角度实现各种黑匣子函数中获得最佳性能,提出了基于深度Q网络(DQN)的贝叶斯变体模型,通过广泛实验,FSAF实现了与最先进的基准相当或更好的遗憾。
贝叶斯优化 (BO) 通常依赖于手工采集函数 (AF) 来顺序确定样本点。然而,在实践中广泛观察到,在不同类型的黑盒函数下,在遗憾方面表现最好的 AF 可能会有很大差异。设计一种能够在各种黑匣子函数中获得最佳性能仍然是一个挑战。本文旨在通过强化少样本 AF 学习 (FSAF) 的角度来应对这一挑战。具体来说,作者首先将 AF 的概念与 Q 函数联系起来,并将深度 Q 网络 (DQN) 视为代理可微分 AF。虽然将 DQN 和现有的小样本学习方法相结合是一个自然的想法,但发现这种直接组合由于严重的过度拟合而表现不佳,这在 BO 中尤其重要,因为需要通用的采样策略。为了解决这个问题,本文提出了一个 DQN 的贝叶斯变体,它具有以下三个特征:(i)它基于 Kullback-Leibler 正则化框架学习 Q 网络的分布作为 AF。这本质上提供了 BO 采样所需的不确定性并减轻了过度拟合。 (ii) 对于贝叶斯 DQN 的先验,作者建议使用由现成 AF 诱导的演示策略,以获得更好的训练稳定性。 (iii) 在元级别,本文利用贝叶斯模型不可知元学习的元损失,它是所提出的 FSAF 的天然伴侣。此外,通过正确设计 Q 网络,FSAF 是通用的,因为它与输入域的维度和基数无关。通过广泛的实验,证明 FSAF 在各种合成和现实世界的测试函数上实现了与最先进的基准相当或更好的遗憾。
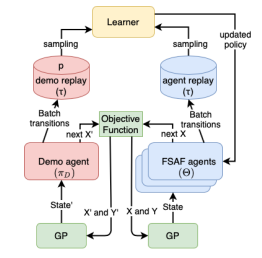
图1 FSAF架构示意图
内容中包含的图片若涉及版权问题,请及时与我们联系删除



评论
沙发等你来抢