ACL 2021 | 当模型压缩遇上量子力学——基于矩阵乘积算符的预训练语言模型轻量化微调

论文标题：Enabling Lightweight Fine-tuning for Pre-trained Language Model Compression based on Matrix Product Operators
论文作者：刘沛羽（中国人民大学）、高泽峰（中国人民大学）、赵鑫（中国人民大学）、谢志远（中国人民大学）、卢仲毅（中国人民大学）、文继荣（中国人民大学）
论文收录：ACL2021 main conference
论文链接：https://arxiv.org/abs/2106.02205
代码链接：https://github.com/RUCAIBox/MPOP

受到量子力学中处理量子多体问题的矩阵乘积算符（MPO）的启发，本文提出了一种新颖的预训练语言模型压缩方法，实现轻量化微调的同时压缩模型参数的效果。

1. 引言

当前预训练语言模型在自然语言处理的多个任务上都取得了显著的效果，并且这种“预训练+微调”的框架已经成为自然语言任务标准的处理流程。在过去的工作中也涌现出了像BERT，GPT等基于Transformer结构的预训练语言模型。虽然这些模型在很多方面都具有出色的表现，但其巨大的参数量限制了模型在小型设备上的应用。因此，为了解决该问题，学术界提出了以参数共享、量化、剪枝和蒸馏为主的模型压缩策略，应用这些策略后得到如ALBERT，MobileBERT以及DistillBERT等压缩模型。

近年来另一种思路也被提出，即固定大部分参数在微调的过程中不更新，从而降低可训练参数的轻量化微调策略，减少下游任务参数微调的成本。

那么针对BERT与GPT这种堆叠Transformer结构的网络，是否可综合两种思路，在压缩模型的同时兼顾轻量化微调，做到模型尽可能小，微调尽可能快呢？

这里为大家介绍一篇ACL2021的研究模型压缩与轻量化微调的工作：《Enabling Lightweight Fine-tuning for Pre-trained Language Model Compression based on Matrix Product Operators》，作者来自中国人民大学高瓴人工智能学院和中国人民大学物理系。

该工作提出基于量子多体问题中的MPO表示的模型压缩与轻量化微调方案–MPOP，在ALBERT成功应用，并在GLUE数据集上进行实验，说明了该方法在模型压缩上的有效性，最终可以减少平均91%的待微调参数量。论文代码和模型均已公布在GitHub网站。

2. 设计动机和方法

预训练语言模型在自然语言处理领域已经取得了非常瞩目的效果，但是由于其庞大的参数量，导致在实际应用的过程中无法高效的微调与应用。因此如何有效压缩预训练语言模型同时在下游任务中高效微调是当前自然语言处理领域最为关心的问题之一。

模型的有效压缩与轻量化微调涉及到对信息的有效提取与利用，模型的信息直接反映在模型的权重矩阵之中，那么如何有效抓住权重矩阵的重要特征就成为解决这类问题的重点方向。在量子多体问题的场景中，MPO可以看做是一种特殊形式的高阶奇异值分解（HOSVD）方法，利用矩阵的特征值来表示信息的重要程度，去除权重矩阵中不重要的噪音来实现模型压缩，同时MPO的张量之间具有非常强的相关性，使得我们可以只更新很少的参数就可以达到全局优化的效果，进而实现轻量化微调。

这种针对矩阵的压缩与轻量化微调的解决方案，可以对已经压缩过的模型进行二次压缩，通用性很强，本文在实验部分对两个主流的压缩模型（MobileBERT和DistilBERT）都进了二次压缩，且得到了很好的效果。

2.1 矩阵的MPO分解

在量子多体物理问题中，MPO分解是一种典型的可以将矩阵分解为一个张量序列的方法。具体为给定矩阵 $M\in\mathbb{R}^{I\times J}$ ，经过MPO分解后可以得到n个张量：

$\mathrm{MPO(M)}=\prod_{k=1}^{n}{\mathcal{T}_{\left(k\right)}\left[d_{k-1},i_k,j_k,d_k\right],}\ (1)$

$\prod_{k=1}^{n}{i_k=I,\ }\prod_{k=1}^{n}{j_k=J,\ }$

其中 $\mathcal{T}_{\left(k\right)}\left[d_{k-1},i_k,j_k,d_k\right]$ 是第k个4阶张量， $i_k$ 和 $j_k$ 是提前设定好的超参数， $d_k$ 称为不同张量之间的连接键，其计算方式为:

$d_k=\min{\left(\prod_{m=1}^{k}{i_m\times j_m},\prod_{m=k+1}^{n}{i_m\times j_m}\right)},\ (2)$

基于MPO表示的形式，本文中定义中间位置的张量为中间张量(central tensor),其余位置的张量称为辅助张量(auxiliary tensors)。根据MPO分解的特性，辅助张量包含的参数远远小于中间张量。

2.2 基于MPO分解的低秩近似

通过前面的方法我们可以对任意矩阵进行分解和重建。参考[1]，我们可以将分解得到的张量之间的连接键 $d_k$ 截断为 ${d_k}^\prime\ (\ {d_k}^\prime<d_k)< span="">dk′ ( dk′<dk)</d_k)<>$

$\epsilon_{k}=\sum_{i=d_{k}-d_{k}^{\prime}}^{d_{k}} \lambda_{i},(3)$

公式中 $\left\{\lambda_i\right\}_{i=1}^{d_k}$ 为对矩阵 $\mathrm{M}\left[i_1j_1\ldots i_kj_k,i_{k+1}j_{k+1}\ldots i_nj_n\right]$ 进行SVD分解后得到的奇异值。我们可以证明，经过MPO分解以及对连接键的截断，原矩阵M变化的误差存在一个理论上界：

$\|M-M P O(M)\|_{F} \leq \sqrt{\sum_{k=1}^{n-1} \epsilon_{k}^{2}},(4)$

基于MPO分解的这个性质，我们可以通过截断连接键实现对原始矩阵M的低秩近似。整体的分解和截断近似示意图如下：

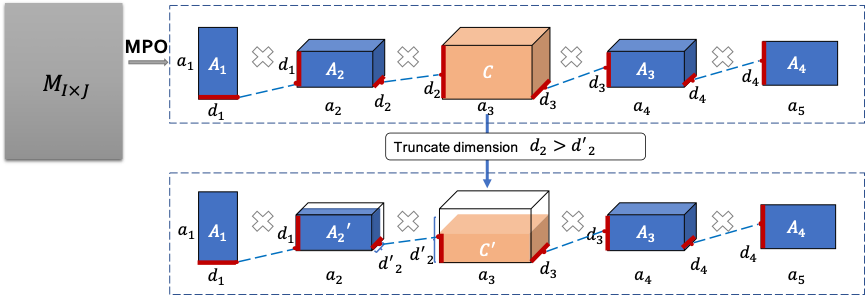
根据前面提到的基于MPO表示的低秩近似特性，已经可以对模型的权重矩阵进行一定程度的压缩。本文基于MPO表示得到的张量参数分布特点，辅助张量仅包含很少的参数，仅更新辅助张量实现轻量化微调，同时对中间张量截断来实现参数压缩。

2.3 基于辅助张量的轻量化微调

首先我们做了一个实验来说明在语言模型的微调阶段，参数更新的幅度是非常小的。从表格中看出，以word embedding矩阵为例，在SST-2任务上微调BERT时候66%的参数变化范围不到1e-4。

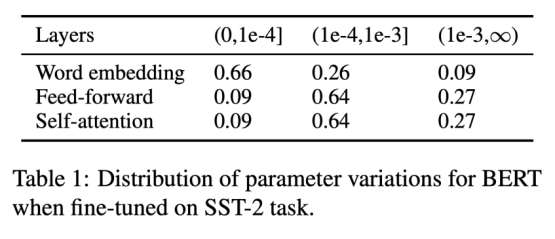
再联系到前面提到的MPO表示的特性，即辅助张量仅仅包含极小部分的参数。因此我们在微调阶段固定中间张量，只更新辅助张量，可以极大减少可训练参数。

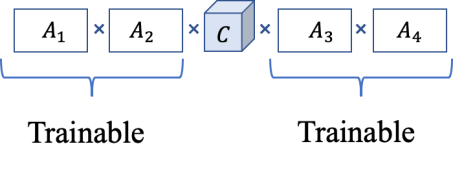
接下来我们从理论上分析一下这种操作的合理性。为此需要引入一个来自量子力学的评估指标–纠缠熵 $S_k$ ，其用来衡量连接键 $d_k$ 中包含的信息：

$S_k=-\sum_{j=1}^{d_k}{v_j\ln{v_j},\ \ \ \ k=1,2,\ldots,n-1},\ (5)$

这里 $v_j$ 表示对 $\mathrm{M}\left[i_1j_1\ldots i_kj_k,i_{k+1}j_{k+1}\ldots i_nj_n\right]$ 进行SVD分解得到的特征值。从计算方法中看出，纠缠熵本质相当于信息熵的变体，把信息熵中的概率替换为SVD分解后得到的奇异值即为纠缠熵。这样就从直观上更容易理解为什么可以用纠缠熵衡量矩阵中包含的信息，因为SVD分解出来的奇异值是和矩阵中包含的信息相关。通过计算，可以发现中间张量附近的连接键纠缠熵最大，这就表明中间张量两侧连接键上所包含的信息最多。

2.4 维度压缩策略

通过截断中间张量可以实现模型的压缩，但是对于Transformer中多层叠加的结构，直接对每一层同时进行压缩，误差会由于这种叠加的结构而指数上升。因此本文提出了一种改进的压缩策略来缓解这个问题。

快速的重构误差评估

为了保证在维度截断后，损失的模型性能可以通过微调进行恢复，就需要保证每次截断只减少最小的重构误差。因此，在对给定权重矩阵使用中间张量进行截断的时候，一次只对引入截断误差最小的矩阵进行维度截断，并且只将其连接键的维度减少1，同时根据公式(3)计算矩阵误差上界可以快速找出引入最小截断误差的矩阵，进而可以找到最小的截断路径。

快速的效果差距评估

为了判断在截断后何时停止，需要评估模型性能的变化，并设定一个阈值 $\Delta$ 来判断模型何时停止截断和训练的操作。因此本文采用前面提到的轻量化微调的方法只训练辅助张量，并且当微调前后的损失函数值差异超过阈值 $\Delta$ 时则停止。

2.5 与同类低秩近似方法的对比

MPO本质上可以看作是一种低秩近似的方法，同类方法还有SVD、CPD和Tucker方法，下表列出了不同低秩近似方法之间的比较结果。这里我们注意到SVD等价于当n=2时MPO分解的特例，而CPD则是当Tucker分解中的核张量是超对角矩阵时候的特例。因此这里只需要做MPO和Tucker两个大类的对比，结果发现，当n>3的时候，MPO有着更低的时间复杂度。

3. 实验与分析

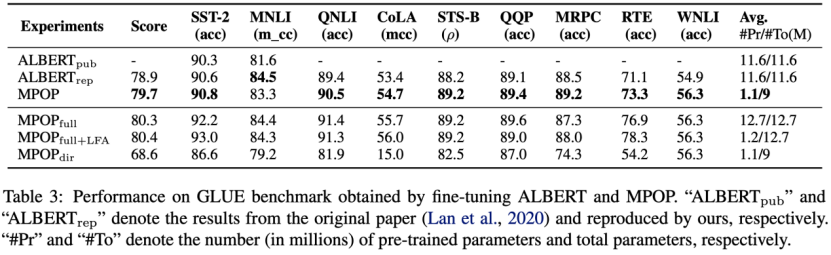
实验中本文以ALBERT模型为基础实现MPOP方法，并在下游的GLUE benchmark上进行微调，实验结果和ALBERT的微调进行对比，发现除了MNLI任务外均取得了超过ALBERT微调的效果，并且总参数降低了22%，可训练参数降低了91%。在消融实验中，为了说明快速微调策略和维度压缩策略的有效性，本文实现了既不经过截断也不使用轻量化微调的MPOP方法（ ${\mathrm{MPOP}}_{\mathrm{full}}$ ），在 ${\mathrm{MPOP}}_{\mathrm{full}}$ 上增加轻量化微调的模型( ${\mathrm{MPOP}}_{\mathrm{full+LFA}}$ )以及不使用维度压缩策略直接进行截断的模型（ ${\mathrm{MPOP}}_{\mathrm{dir}}$ ）。通过对比 ${\mathrm{MPOP}}_{\mathrm{dir}}$ 和 $\mathrm{MPOP}$ 发现，直接截断中间张量会由于一次性损失太多信息而无法通过训练恢复精度，另一方面对比 ${\mathrm{MPOP}}_{\mathrm{full+LFA}}$ 和 ${\mathrm{MPOP}}_{\mathrm{full}}$ 发现，直接微调更多的参数反而会在一些任务上会导致模型性能下降（比如RTE和MRPC这样的小数据集任务）。

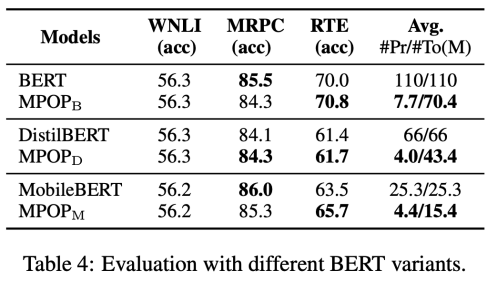
上面的表格中，本文补充了使用MPOP方法在BERT以及使用蒸馏方法压缩BERT模型的变种，比如DistilBERT和MobileBERT，发现MPOP均可以明显降低模型的可训练参数。

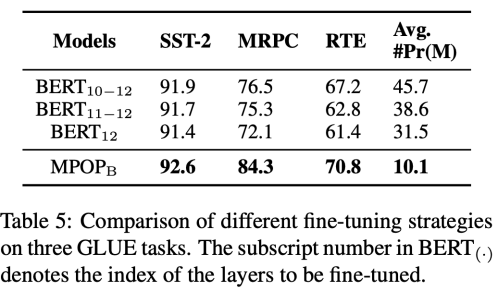
这里采用仅微调BERT个别层的方法与快速微调方法进行对比，发现本文提出的轻量化微调策略会覆盖微调所有的层，但可训练参数却更低且效果更好。

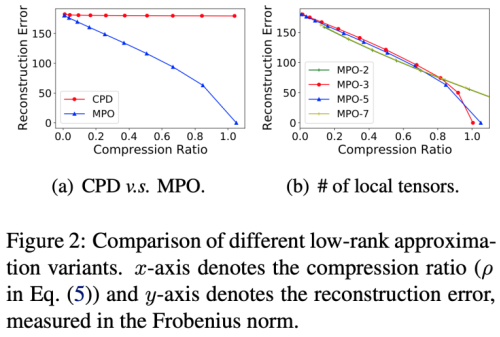
上面的图(a)中对比了CPD和MPO方法的压缩效果，发现在同样的压缩率条件下，MPO有着更低的重构误差，在图(b)中，我们测试了MPO展开成的张量的数目对重构误差的影响，结果发现，采用2,3,5,7不同的张量数目，并不会对重构误差有明显的影响。

4. 总结

本文提出了一种基于MPO表示的预训练语言模型压缩的方法，基于MPO表示的权重矩阵由中间张量（包含大部分参数）和辅助张量（包含很少的参数）组成，在本文中我们通过理论分析与实验对比，证明了仅更新辅助张量实现轻量化微调可以极大降低可训练参数，通过维度挤压策略可以截断中间张量实现压缩总参数的目标。本文首次使用来源于量子多体问题中的MPO表示用于预训练语言模型的压缩，并为模型压缩提供了新的解决思路。

参考文献：

[1] Ze-Feng Gao, Song Cheng, Rong-Qiang He, ZY Xie, Hui-Hai Zhao, Zhong-Yi Lu, and Tao Xiang. 2020. Compressing deep neural networks by ma- trix product operators. Physical Review Research, 2(2):023300.

内容中包含的图片若涉及版权问题，请及时与我们联系删除