编者按：“几何深度学习”先驱、牛津大学DeepMind教授Michael Bronstein 最近在博客继续更新了其系列长文《迈向几何深度学习》的第2篇：感知器事件（参阅：《迈向几何深度学习》第1篇：站在巨人的肩膀上）。下文是对它的编译。

几何深度学习从对称性和不变性的角度来研究广泛的 ML 问题，为 CNN、GNN 和 Transformers 等各种神经网络架构提供了通用蓝图。我们在发表的一系列新文章，研究了可追溯到古希腊的几何思想，如何塑造了现代深度学习。

在“迈向几何深度学习”系列的第二篇文章中，我们将讨论早期的神经网络模型，以及针对它们的批评如何开拓出了计算几何的新领域。这篇文章基于M. M. Bronstein，J. Bruna，T. Cohen和P. Veličković 合著的《Geometric Deep Learning》（完稿后将由麻省理工学院出版社出版）书的介绍章节，以及我们开设的非洲机器智能硕士（AMMI）课程内容。请参阅我们讨论对称性的第一篇文章，以及已经总结的关于几何深度学习概念的文章。

“人工智能”作为一个科学领域，我们很难就它诞生的具体时间点达成一致（本质而言，人类一直痴迷于理解智能、汲取文明之光），我们将尝试一个风险较小的切入点，把研究深度学习的前身，作为我们讨论的主要话题。这段历史可以压缩到不到一个世纪。

 

感知器的兴衰

到了20世纪30年代，一个知见已经变得显而易见了：心灵存在于大脑中，科学家们也开始从大脑网络结构的角度，研究和解释大脑功能，如记忆，感知和推理。McCulloch和Pitts [1]被认为是神经元的第一个数学抽象，并展示了它计算逻辑函数的能力。就在传奇的达特茅斯学院研讨会创造了“人工智能”[2]这个词的一年后，来自康奈尔航空实验室的美国心理学家弗兰克·罗森布拉特（Frank Rosenblatt）提出了一种他称之为“感知器”的神经网络[3]。


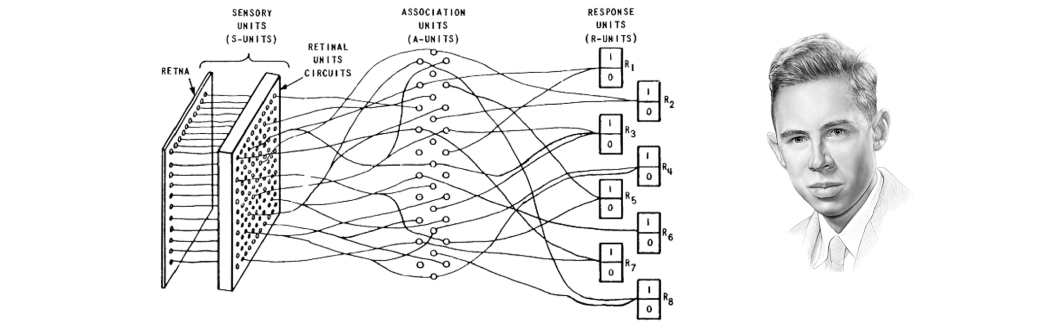
Frank Rosenblatt在康奈尔航空实验室开发了Mark I 感知器神经网络，用于简单的视觉模式识别任务。绘画：伊霍尔·戈尔斯基。

感知器首先实现于数字机器，然后是专用硬件，并设法解决了简单的模式识别问题，例如几何形状的分类。然而，“联结主义”（AI研究者自己做标注的人工神经网络算法）迅速崛起后，却被马文·明斯基（Marvin Minsky）和西摩·帕佩特（Seymour Papert）那臭名昭著的书《感知器》（Perceptrons），兜头浇了一桶冷水[4]。

因为第一次“AI冬天”导致神经网络沉寂了10多年，在深度学习社区中，人们通常会追溯性地指责明斯基和帕佩特。他们著作一个典型的叙述便是“异或事件”，这“证明”了感知器甚至无法学习非常简单的逻辑功能。某些消息来源甚至加了些戏剧性：回忆罗森布拉特和明斯基曾上过同一所学校，甚至声称罗森布拉特于1971年一次划船事故中的遇难，其实是研究工作遭到同事批评之后的自杀。

Marvin Minsky和Seymour Papert，著名图书“Perceptrons”作者。书封面上的两个形状（其中一个是相连的）暗示了“奇偶校验问题”。这本书考虑了简单的单层感知（左上），包括引入群不变性（左下角）也许是最早的几何学习方法。

现实可能更平凡，也更微妙。首先，导致美国“人工智能之冬”的一个更合理原因是1969年的曼斯菲尔德修正案，该修正案要求军方资助“以任务为导向的直接研究，而不是基础性的无方向研究”。当时人工智能领域的许多工作，包括罗森布拉特的研究，都是由军事机构资助的，并没有立即显示出效用，由此导致的资金削减产生了巨大的影响。其次，神经网络和人工智能总体上被过度炒作了，让人回想起1958年《纽约客》的一篇文章，称感知器是：

“有史以来第一个与人类大脑相媲美的劲敌”——《纽约客》（The New Yorker，1958）

以及“非凡的机器”、“能够达到思想”[5]，或者过度自信的MIT夏季视觉项目期望“构建视觉系统的重要部分”，并在1966年夏季学期内实现“模式识别”的能力[6]。研究界意识到，最初“解决智能问题”的期望过于乐观，尚需待以时日。

早期炒作：《纽约客》1958年一篇文章称赞感知器“能够思考”（左），而过于乐观的“麻省理工学院夏季视觉项目”旨在1966年几个月内构建“视觉系统的重要组成部分”。

如果人们研究了争议的实质，会发现显而易见的事实是，罗森布拉特所说的“感知器”与明斯基和帕佩特的理解有很大不同。明斯基和帕佩特将分析和批评集中在某类狭窄的单层神经网络上，并称之为“简单感知器”（和现代术语关系密切），该网络计算用一个非线性函数输入的加权线性组合[7]。另一方面，罗森布拉特则考虑了更广泛的架构类别，这些架构早于现在被视作“现代”深度学习的许多想法，包括具有随机和本地连接的多层网络[8]。

如果罗森布拉特知道弗拉基米尔·阿诺德和安德烈·科尔莫哥洛夫[10-11]证明了第13个希尔伯特问题[9]——方式是建立了一个连续多元函数（可以写成单个变量的连续函数叠加），可能会反驳一些关于感知器表现力的批评。阿诺德-柯尔莫哥洛夫定理是多层（或“深度”）神经网络“通用逼近定理”的前身，后者解决了感知器被诟病的那些问题。

明斯基和帕佩特的书，最被人熟知的便是切断了早期的灵感萌芽，对神经网络发展机遇丧失起了推波助澜的作用；但被世人所忽视的一个重要方面，是它第一次提出了针对学习问题的几何分析。这一事实反映在这本书的副标题中——“计算机几何学导论”。当时对本书的一个批判性评论（本质是为罗森布拉特辩护）问道：

”计算几何“这门新学科是否会成长为一个活跃的数学领域？还是会在一堆死胡同中逐渐消失？“——布洛克（1970）

前者发生了：计算几何现在已经是一个成熟的领域[13]。此外，明斯基和帕佩特可能令人称道的地方，是将群论首次引入机器学习领域：他们的群不变性定理指出，如果神经网络对某个群是不变的，那么它的输出可以表示为群轨道的函数。虽然他们用这个结果来证明感知器可以学习的局限性，但随后Shun'ichi Amari [14]也使用了类似的方法来构建模式识别问题中的不变特征。这些想法在Terrence Sejnowski[15]和John Shawe-Taylor[16-17]作品中经过了一番演变，为几何深度学习蓝图奠定了基础，但令人遗憾的是今天很少被引用。

 

普遍逼近和维度的诅咒

前面提到的通用逼近概念值得进一步讨论。该术语指将任何连续多元函数近似为任何所需精度的能力；在机器学习文献中，这种类型的结果通常归功于Cybenko [18]和Hornik [19]。与明斯基和帕佩特批评的“简单”（单层）感知器不同，多层神经网络是泛逼近器，因此对于机器学习是一种有吸引力的架构。我们可以将有监督机器学习视为函数逼近问题：给定训练集上某些未知函数（例如，图像分类器）的输出（例如，猫和狗的图像），我们尝试从某个假设类中找到一个函数，这个函数非常适合训练数据，并允许预测输入数据不可见的结果输出（“泛化”）。

迈向通用逼近：由安德烈·柯尔莫哥洛夫和弗拉基米尔·阿诺德对大卫·希尔伯特第13个问题的证明，最早表明这一结论的成果之一：元连续函数可表示为简单一维函数的组合、和。George Cybenko和Kurt Hornik证明了神经网络特有的结果，表明具有一个隐藏层的感知器可以将任何连续函数逼近为任何所需的精度。

通用逼近使得我们可以通过多层神经网络，用非常广泛的正则性类（连续函数）来表达函数。换句话说，存在一个具有一定数量的神经元和某些权重的神经网络，该神经网络逼近于从输入到输出空间（例如，从图像空间到标签空间）的给定函数映射。然而，通用逼近定理并没有告诉我们如何找到这样的权重。事实上，神经网络中的学习（即寻找权重）在早期一直是个巨大的挑战。

罗森布拉特则展示了一种仅针对单层感知器的学习算法；后来为了训练多层神经网络，Aleksey Ivakhnenko和Valentin Lapa [20]使用了一种称为“数据处理的组方法”的逐层学习算法。这使得Ivakhnenko [21]的研究能够深入到八层 ——这在1970年代初是一项了不起的壮举！

如何训练你的神经网络？现在无处不在的反向传播，直到1980年代David Rumelhart的论文问世之后才成为标准（尽管Paul Werbos和Seppo Linnainmaa之前就已经作了介绍）。早期的方法，如Aleksey Ivakhnenko的“数据处理的组方法”，在1970年代初就允许训练深度神经网络。

一个突破来自反向传播的发明，这是一种使用链规则来计算权重相对于损失函数的梯度的算法，并允许使用基于梯度下降的优化技术来训练神经网络。截止今天，这还是深度学习的标准方法。虽然反向传播的起源至少可追溯到1960年[22]，但这种方法在神经网络中的第一个令人信服的证明，来自Rumelhart，Hinton和Williams一篇被广泛引用的Nature论文[23]。这个简单高效的算法引入是神经网络得以在1980年代和1990年代重返AI场景的关键。

从逼近理论的视角来观察神经网络，会导致一些愤世嫉俗者将深度学习称为“美化曲线拟合”。我们将尝试回答一个重要问题来让读者判断这个格言有多真实：需要多少样本（训练示例）才能准确逼近一个函数？逼近理论家会立即反驳说，多层感知器可以表示的连续函数类显然太大了：人们可以通过有限的点集合传递无限多个不同的连续函数[24]。有必要施加额外的正则性假设，例如Lipschitz连续性[25]，在这种情况下，我们可以提供所需样本数的界限。

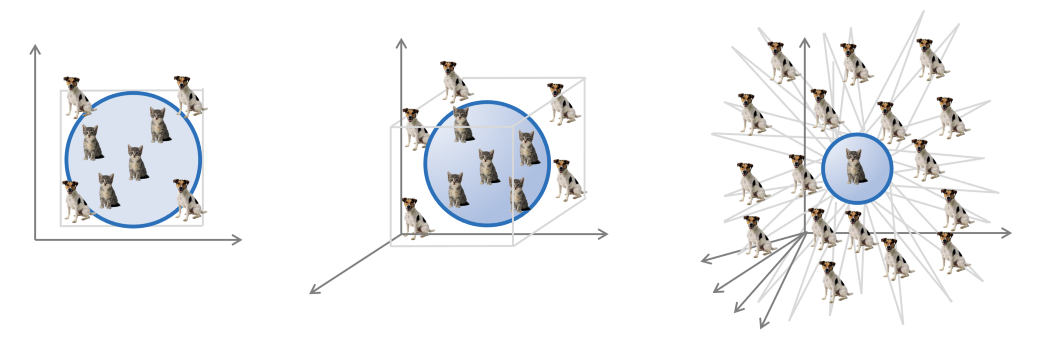
维数诅咒是一种发生在高维空间中的几何现象。可视化它的一种方法是查看刻在一单位超立方体中的一单位球的体积比例（后者表示特征空间，而前者可以解释为“最近邻”分类器）。体积比随维度呈指数级衰减：对于 d=2，该比率为 ~0.78，对于 d=3，它下降到 ~0.52，对于 d=10，它已经是 ~0.01。图：改编自Vision Dummy。

不幸的是，这些边界伴随着维度的增加而呈指数级扩展——这种现象俗称“维度之咒”[26] - 这在机器学习问题中是不可接受的：即使是小规模的模式识别问题，如图像分类，也需要处理数千个维度的输入空间。如果人们不得不依靠逼近理论的典型结果，就不可能通过机器学习实现。在我们的插图中，为了学会区分它们，理论上需要的猫和狗图像的例子数量将远远大于宇宙中原子的数量[27] ——周围根本没有足够的猫和狗来做到这一点。

维度之咒：逼近理论的标准结果不能很好地与维度一起缩放。因此，即使在简单的机器学习任务中，人们也会预测训练样本的数量将明显大于实际可能的数量。

 

AI冬天来了

英国数学家詹姆斯·莱特希尔爵士（Sir James Lighthill）在一篇论文中提出了机器学习方法扩展到高维的一番挣扎，人工智能历史学家称之为“Lighthill报告”[28]，其中他使用了“组合爆炸”一词，声称现有的人工智能方法只能解决玩具性质的问题，而在现实世界的应用中会变得很棘手。

“人工智能以及相关领域的大多数工作者都承认，他们对过去二十五年来取得的成就感到失望。[……]到目前为止，该领域的任何部分都没有产生当时承诺的重大影响“——詹姆斯·莱特希尔爵士（Sir James Lighthill，1972）

由于Lighthill报告是受英国科学研究委员会委托，评估人工智能领域的学术研究，所以其悲观的结论导致投入AI领域的资金削减。再加上美国资助机构的类似决定，这些都是导致1970年代人工智能研究陷入沉寂的破坏因子。

对我们来说，意识到经典函数分析不能提供充分的框架来处理机器学习问题，将是寻求更强的几何形式规律的动力，这种规律可以在神经网络的特定布线中实现 ——例如卷积神经网络的局部连通性。公平地说，我们十年前目睹过的深度学习胜利得以重新出现，至少部分归功于这些见解。

参考文献

[1] W. S. McCulloch and W. Pitts, A logical calculus of the ideas immanent in nervous activity (1943), The Bulletin of Mathematical Biophysics 5(4):115–133.

[2] The Dartmouth Summer Research Project on Artificial Intelligence was a 1956 summer workshop at Dartmouth College that is considered to be the founding event of the field of artificial intelligence.

[3] F. Rosenblatt, The perceptron, a perceiving and recognizing automaton (1957), Cornell Aeronautical Laboratory. The name is a portmanteau of ‘perception’ and the Greek suffix -τρον denoting an instrument.

[4] M. Minsky and S. A. Papert, Perceptrons: An introduction to computational geometry (1969), MIT Press.

[5] That is why we can only smile at similar recent claims about the ‘consciousness’ of deep neural networks: אין כל חדש תחת השמש.

[6] Sic in quotes, as “pattern recognition” has not yet become an official term.

[7] Specifically, Minsky and Papert considered binary classification problems on a 2D grid (‘retina’ in their terminology) and a set of linear threshold functions. While the inability to compute the XOR function is always brought up as the main point of criticism in the book, much of the attention was dedicated to geometric predicates such as parity and connectedness. This problem is alluded to on the cover of the book, which is adorned by two patterns: one is connected, and another one is not. Even for a human, it is very difficult to determine which is which.

[8] E. Kussul, T. Baidyk, L. Kasatkina, and V. Lukovich, Rosenblatt perceptrons for handwritten digit recognition (2001), IJCNN showed that Rosenblatt’s 3-layer perceptrons implemented on the 21st-century hardware achieve an accuracy of 99.2% on the MNIST digit recognition task, which is on par with modern models.

[9] Hilbert’s Thirteenth Problem is one of the 23 problems compiled by David Hilbert in 1900 and entailing the proof of whether a solution exists for all 7th-degree equations using continuous functions of two arguments. Kolmogorov and his student Arnold showed a solution of a generalised version of this problem, which is now known as the Arnold–Kolmogorov Superposition Theorem.

[10] В. И. Арнольд, О представлении непрерывных функций нескольких переменных суперпозициями непрерывных функций меньшего числа переменных (1956), Доклады Академии Наук СССР 108:179–182.

[11] В. И. Арнольд, О функции трех переменных (1957), Доклады Академии Наук СССР 114:679–681.

[12] H. D. Block, A review of “Perceptrons: An introduction to computational geometry” (1970), Information and Control 17(5): 501–522.

[13] Computational Geometry has subject code I.3.5 in the ACM Computing Classification System.

[14] S.-I. Amari, Feature spaces which admit and detect invariant signal transformations (1978), Joint Conference on Pattern Recognition.

[15] T. Sejnowski et al., Learning symmetry groups with hidden units: Beyond the perceptron (1986), Physica D: Nonlinear Phenomena 22(1–3):260–275.

[16] J. Shawe-Taylor, Building symmetries into feedforward networks (1989), ICANN.

[17] J. Shawe-Taylor, Symmetries and discriminability in feedforward network architectures (1993), IEEE Trans. Neural Networks 4(5): 816–826.

[18] G. Cybenko, Approximation by superpositions of a sigmoidal function (1989), Mathematics of Control, Signals and Systems 2(4):303–314.

[19] K. Hornik, Approximation capabilities of multilayer feedforward networks (1991) Neural Networks 4(2):251–257.

[20] А. Г. Ивахненко, В. Г. Лапа, Кибернетические предсказывающие устройства (1965), Наукова думка.

[21] A. Ivakhnenko, Polynomial theory of complex systems (1971), IEEE Trans. Systems, Man, and Cybernetics 4:364–378.

[22] Backpropagation is based on the chain rule of differentiation that itself goes back to the co-inventor of differential calculus Gottfried Wilhelm von Leibniz in 1676. A precursor of backpropagation was used by H. J. Kelley, Gradient theory of optimal flight paths (1960), Ars Journal 30(10): 947–954 to perform optimisation of complex nonlinear multi-stage systems. Efficient backpropagation that is still in use today was described in the Finnish master’s thesis of S. Linnainmaa, Algoritmin kumulatiivinen pyoristysvirhe yksittaisten pyoristysvirheiden taylor-kehitelmana (1970), University of Helsinki. The earliest use in neural networks is due to P. J. Werbos, Applications of advances in nonlinear sensitivity analysis (1982), System Modeling and Optimization 762–770, Springer, which is usually cited as the origin of the method. See J. Schmidhuber, Deep learning in neural networks: An overview (2015), Neural Networks 61:85–117.

[23] D. E. Rumelhart et al., Learning representations by back-propagating errors (1986), Nature 323(6088):533–536.

[24] There are even examples of continuous nowhere differentiable functions such as the construction of Weierstrass (1872).

[25] Roughly, Lipschitz-continuous functions do not arbitrarily shrink or expand the distance between points on the domain. For differentiable functions, Lipschitz continuity can be expressed as an upper bound on the norm of the gradient, implying that the function does not ‘jump’ too abruptly.

[26] The first to use the term was Richard Bellman in the preface of his 1957 book Dynamic Programming, where he refers to dimensionality as “a curse which has hung over the head of the physicist and astronomer for many a year.”

[27] The number of protons in the observable universe, known as the Eddington number, is estimated at 10⁸⁰.

[28] J. Lighthill, Artificial intelligence: A general survey (1973) Artificial Intelligence 1–21, Science Research Council London.

The portraits of Rosenblatt, Minsky, and Papert were hand-drawn by Ihor Gorskiy. Detailed lecture materials on Geometric Deep Learning are available on the project webpage. See Michael’s other posts in Towards Data Science, subscribe to his posts, get Medium membership, or follow Michael, Joan, Taco, and Petar on Twitter.